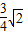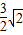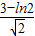题目内容
若点P是曲线y=2-lnx上任意一点,则点P到直线y=-x的最小距离是
- A.

- B.

- C.
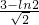
- D.
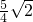
B
分析:利用导数研究函数的极值和最值、点到直线的距离公式即可得出.
解答:设点P(x,2-lnx)为曲线y=2-lnx上任意一点,则点P到直线y=-x的距离d=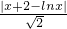 ,
,
令f(x)=x+2-lnx(x>0),则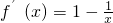 =
= ,令f′(x)=0,解得x=1.
,令f′(x)=0,解得x=1.
当x>1时,f′(x)>0,函数f(x)单调递增;当0<x<1时,f′(x)<0,函数f(x)单调递减.
∴当x=1时,函数f(x)取得极小值,也是最小值,且f(1)=3>0.
∴点P到直线y=-x的最小距离d=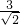 =
= .
.
故选B.
点评:整理掌握利用导数研究函数的极值和最值、点到直线的距离公式是解题的关键.
分析:利用导数研究函数的极值和最值、点到直线的距离公式即可得出.
解答:设点P(x,2-lnx)为曲线y=2-lnx上任意一点,则点P到直线y=-x的距离d=
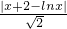 ,
,令f(x)=x+2-lnx(x>0),则
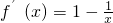 =
= ,令f′(x)=0,解得x=1.
,令f′(x)=0,解得x=1.当x>1时,f′(x)>0,函数f(x)单调递增;当0<x<1时,f′(x)<0,函数f(x)单调递减.
∴当x=1时,函数f(x)取得极小值,也是最小值,且f(1)=3>0.
∴点P到直线y=-x的最小距离d=
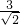 =
= .
.故选B.
点评:整理掌握利用导数研究函数的极值和最值、点到直线的距离公式是解题的关键.

练习册系列答案
相关题目