题目内容
5.“m=±1”是“复数(1-m2)+(1+m)i(其中i是虚数单位)为纯虚数”的( )| A. | 充要条件 | B. | 充分而不必要条件 | ||
| C. | 必要而不充分条件 | D. | 既不充分也不必要条件 |
分析 根据充分条件和必要条件的定义结合纯虚数的概念进行判断即可.
解答 解:若复数(1-m2)+(1+m)i为纯虚数,
则满足{1−m2=01+m≠0,即{m=±1m≠−1,
解得m=1,
当m=-1时,复数(1-m2)+(1+m)i=0为实数,不是纯虚数,
即“m=±1”是“复数(1-m2)+(1+m)i(其中i是虚数单位)为纯虚数”的必要不充分条件,
故选:C
点评 本题主要考查充分条件和必要条件的判断,根据纯虚数的概念是解决本题的关键.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
13.将函数y=sin(2x-\frac{π}{3})的图象向右平移\frac{7π}{12}个单位,再将图象上每个点的横坐标扩大到原来的2倍,纵坐标不变,得到的图象对应的函数表达式是( )
| A. | y=sin(x+\frac{5}{6}π) | B. | y=cosx | C. | y=sin(4x+\frac{5}{6}π) | D. | y=cos4x |
10.命题“对任意的x∈R,x2≥0”的否定是( )
| A. | 对任意的x∈R,x2<0 | B. | 不存在x∈R,x2<0 | ||
| C. | 存在x∈R,x2<0 | D. | 存在x∈R,x2≥0 |

 如图,在平面直角坐标系xOy中,A和B分别是椭圆C1:
如图,在平面直角坐标系xOy中,A和B分别是椭圆C1: 如图为一多面体ABCDFE,AB⊥AD,AB∥CD,CD=2AB=2AD=4,
如图为一多面体ABCDFE,AB⊥AD,AB∥CD,CD=2AB=2AD=4,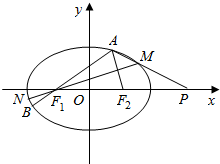 已知椭圆C:
已知椭圆C: