题目内容
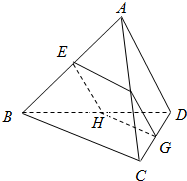 空间四边形ABCD的对棱AD,BC成60°的角,且AD=BC=a,平行于AD与BC的截面分别交AB,AC,CD,BD于E、F、G、H.
空间四边形ABCD的对棱AD,BC成60°的角,且AD=BC=a,平行于AD与BC的截面分别交AB,AC,CD,BD于E、F、G、H.(1)求证:四边形EFGH为平行四边形;
(2)E在AB的何处时截面EFGH的面积最大?最大面积是多少?
分析:(1)证明BC∥EF,EF∥HG.然后证明四边形EFGH为平行四边形.
(2)设
=x,求出EH=(1-x)a.推出S四边形EFGH=EF•EH•sin60°=
a2.推出E为AB的中点时,截面EFGH的面积最大为
a2.
(2)设
| AE |
| AB |
| ||
| 8 |
| ||
| 8 |
解答:证明:(1)∵BC∥平面EFGH,BC?平面ABC,平面ABC∩平面EFGH=EF,
∴BC∥EF,同理BC∥HC,
∴EF∥HG.
同理可证EH∥FG,
∴四边形EFGH为平行四边形.
解:(2)∵AD与BC成角为60°,
∴∠HEF=60°(或120°),设
=x,
∵
=
=x,BC=a,
∴EF=ax,由
=
=
,得EH=(1-x)a.
∴S四边形EFGH=EF•EH•sin60°
=ax•a(1-x)•
=
a2•x(1-x)≤
a2•(
)2=
a2.
当且仅当x=1-x,即x=
时等号成立,即E为AB的中点时,截面EFGH的面积最大为
a2.
∴BC∥EF,同理BC∥HC,
∴EF∥HG.
同理可证EH∥FG,
∴四边形EFGH为平行四边形.
解:(2)∵AD与BC成角为60°,
∴∠HEF=60°(或120°),设
| AE |
| AB |
∵
| EF |
| BC |
| AE |
| AB |
∴EF=ax,由
| EH |
| AD |
| BE |
| AB |
| 1-x |
| 1 |
∴S四边形EFGH=EF•EH•sin60°
=ax•a(1-x)•
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| x+1-x |
| 2 |
| ||
| 8 |
当且仅当x=1-x,即x=
| 1 |
| 2 |
| ||
| 8 |
点评:本题考查几何图形的证明与判定,几何体体积的求法,考查计算能力.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
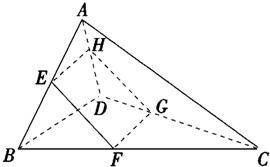 空间四边形ABCD的两条对棱AC、BD的长分别为5和4,则平行于两条对棱的截面四边形EFGH在平移过程中,周长的取值范围是
空间四边形ABCD的两条对棱AC、BD的长分别为5和4,则平行于两条对棱的截面四边形EFGH在平移过程中,周长的取值范围是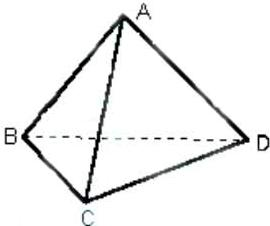 如图,一空间四边形ABCD的对边AB与CD,AD与BC都互相垂直,用向量证明:AC与BD也互相垂直.
如图,一空间四边形ABCD的对边AB与CD,AD与BC都互相垂直,用向量证明:AC与BD也互相垂直.