题目内容
已知空间四边形ABCD的各边及对角线相等，AC与平面BCD所成角的余弦值是
．
| ||
| 3 |
| ||
| 3 |
分析：由题意可得多面体ABCD为正四面体，设点A在平面BCD内的射影为O，则O是等边△BCD的中心，∠ACO为AC与平面BCD所成角．在Rt△AOC中，根据cos∠ACO=
求出．
| CO |
| AC |
解答：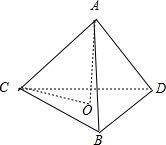
解：由题意可得多面体ABCD为正四面体，设点A在平面BCD内的射影为O，则O是等边△BCD的中心，∠ACO为AC与平面BCD所成角．
设正四面体的棱长为1，则OC=
×
CB=
．
Rt△AOC中，cos∠ACO=
=
故答案为：
解：由题意可得多面体ABCD为正四面体，设点A在平面BCD内的射影为O，则O是等边△BCD的中心，∠ACO为AC与平面BCD所成角．设正四面体的棱长为1，则OC=
| 2 |
| 3 |
| ||
| 2 |
| ||
| 3 |
Rt△AOC中，cos∠ACO=
| CO |
| AC |
| ||
| 3 |
故答案为：
| ||
| 3 |
点评：本题考查直线和平面所成的角的定义和求法，找出直线和平面所成的角，是解题的关键．
练习册系列答案
相关题目
如图，已知空间四边形ABCD中，BC=AC，AD=BD，E是AB的中点．
如图，已知空间四边形ABCD中，BC=AC，AD=BD，E是AB的中点．
如图，已知空间四边形ABCD中，BC=AC，AD=BD，E是AB的中点，求证：
