题目内容
下列命题:
(1)在△ABC中,“A<B”是“sinA<sinB”的必要而非充分条件;
(2)函数f(x)=|sinx-cosx|的最小正周期是π;
(3)在△ABC中,若AB=2
,AC=2
,B=
,则△ABC为钝角三角形;
(4)要得到函数y=sin(
-
)的图象,只需将y=sin
的图象向右平移
个单位.
其中真命题的序号是
(1)在△ABC中,“A<B”是“sinA<sinB”的必要而非充分条件;
(2)函数f(x)=|sinx-cosx|的最小正周期是π;
(3)在△ABC中,若AB=2
| 2 |
| 3 |
| π |
| 3 |
(4)要得到函数y=sin(
| x |
| 2 |
| π |
| 4 |
| x |
| 2 |
| π |
| 4 |
其中真命题的序号是
(2)
(2)
.分析:(1)分A、B均为锐角和一锐角一钝角由A<B推出sinA<sinB,再由sinA<sinB,移向后利用三角函数的和差化积公式,结合角的范围推出A<B;
(2)把给出的函数绝对值内的部分化积,求得周期为2π,加绝对值后图象在x轴下方的部分进行了反折,使函数周期变为原来的一半;
(3)在三角形中运用正弦定理,结合大边对大角求出角C,从而求出角A,可以得到三角形的形状;
(4)把给出的函数式y=sin(
-
)变形为y=sin
(x-
),由变量x的变化可以得到答案.
(2)把给出的函数绝对值内的部分化积,求得周期为2π,加绝对值后图象在x轴下方的部分进行了反折,使函数周期变为原来的一半;
(3)在三角形中运用正弦定理,结合大边对大角求出角C,从而求出角A,可以得到三角形的形状;
(4)把给出的函数式y=sin(
| x |
| 2 |
| π |
| 4 |
| 1 |
| 2 |
| π |
| 2 |
解答:解:(1)在△ABC中,若A,B均为锐角,由A<B⇒sinA<sinB.若A为锐角,B为钝角,因为A+B<π,
所以A<π-B<
,所以sinA<sin(π-B)=sinB.反之,在△ABC中,若sinA<sinB,则sinA-sinB<0,
即sin
cos
<0,因为0<A<π,0<B<π,0<A+B<π,所以-
<
<
,0<
<
,
所以cos
>0,则sin
<0,所以A-B<0,即A<B.
所以,在△ABC中,“A<B”是“sinA<sinB”的充要条件.所以,(1)不正确;
(2)由f(x)=|sinx-cosx|=|sin(x-
)|,因为函数y=sin(x-
)的周期为2π,所以,函数f(x)=|sinx-cosx|的最小正周期是π.所以(2)正确;
(3)在△ABC中,由
=
,因为AB=2
,AC=2
,B=
,所以
=
,
解得:sinC=
,由三角形中大边对大角知C=
.所以A=π-(
+
)=
.
所以△ABC为锐角三角形.所以(3)不正确;
(4)函数y=sin(
-
)=sin
(x-
),所以,要得到函数y=sin(
-
)的图象,只需将y=sin
的图象向右平移
个单位.所以,(4)不正确.
故真命题的序号是(2).
故答案为(2).
所以A<π-B<
| π |
| 2 |
即sin
| A-B |
| 2 |
| A+B |
| 2 |
| π |
| 2 |
| A-B |
| 2 |
| π |
| 2 |
| A+B |
| 2 |
| π |
| 2 |
所以cos
| A+B |
| 2 |
| A-B |
| 2 |
所以,在△ABC中,“A<B”是“sinA<sinB”的充要条件.所以,(1)不正确;
(2)由f(x)=|sinx-cosx|=|sin(x-
| π |
| 4 |
| π |
| 4 |
(3)在△ABC中,由
| AC |
| sinB |
| AB |
| sinC |
| 2 |
| 3 |
| π |
| 3 |
2
| ||
sin
|
2
| ||
| sinC |
解得:sinC=
| ||
| 2 |
| π |
| 4 |
| π |
| 3 |
| π |
| 4 |
| 5π |
| 12 |
所以△ABC为锐角三角形.所以(3)不正确;
(4)函数y=sin(
| x |
| 2 |
| π |
| 4 |
| 1 |
| 2 |
| π |
| 2 |
| x |
| 2 |
| π |
| 4 |
| x |
| 2 |
| π |
| 2 |
故真命题的序号是(2).
故答案为(2).
点评:本题考查了命题的真假判断与应用,结合三角函数广泛考查了充要条件、函数的周期、函数图象的平移及解三角形问题,本题中的四个命题在判断时各有易错点,命题(1)由A<B推sinA<sinB时学生不易想到讨论,命题(2)往往忽略绝对值对周期的影响,命题(3)中大边对大角是关键,命题(4)是看变量x的变化,此题属中档以上题.

练习册系列答案
相关题目
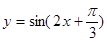 的图象向右平移
的图象向右平移 个单位,得到函数y=sin2x的图象;
个单位,得到函数y=sin2x的图象; 的图象和函数
的图象和函数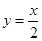 的图象有三个公共点;
的图象有三个公共点;