题目内容
若等差数列{an}的前5项之和S5=25,且a2=3,则a7=( )
| A.12 | B.13 | C.14 | D.15 |
B
解析试题分析:根据等差数列的求和公式和通项公式分别表示出S5和a2,联立方程求得d和a1,最后根据等差数列的通项公式求得答案.即根据题意,有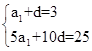 ,故可知d=2,a1=1,∴a7=1+6×2=13,故答案为:13
,故可知d=2,a1=1,∴a7=1+6×2=13,故答案为:13
考点:等差数列的性质
点评:本题主要考查了等差数列的性质.考查了学生对等差数列基础知识的综合运用.属于基础题。

练习册系列答案
相关题目
各项都为正数的等比数列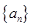 的公比
的公比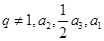 成等差数列,则
成等差数列,则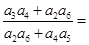 ( )
( )
A.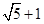 | B.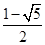 | C.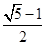 | D. |
等差数列{an}共有2n+1项,其中奇数项之和为4,偶数项之和为3,则n的值是
| A.3 | B.5 | C.7 | D.9 |
在等差数列 中,已知
中,已知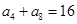 ,则该数列前11项和
,则该数列前11项和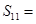 ( )
( )
| A.58 | B.88 | C.143 | D.176 |
在等差数列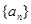 中,
中,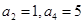 ,则
,则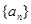 的前5项和
的前5项和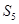 =( )
=( )
| A.7 | B.15 | C.20 | D.25 |
已知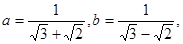 则
则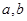 的等差中项为( )
的等差中项为( )
A. | B.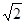 | C.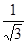 | D.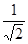 |
在等差数列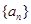 中,若
中,若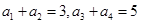 ,则
,则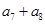 的和等于 ( )
的和等于 ( )
| A.7 | B.8 | C.9 | D.10 |
在等差数列{an}中,若a3+a4+a5+a6+a7=450,则a2+a8的值等于( )
| A.45 | B.75 | C.180 | D.300 |
设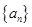 是等差数列,且
是等差数列,且 ,则这个数列的前5项和
,则这个数列的前5项和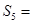 ( )
( )
| A.10 | B.15 | C.20 | D.25 |