题目内容
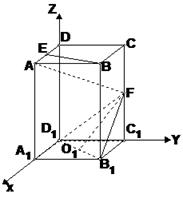
已知长方体ABCD—A1B1C1D1中,AB=BC=4,AA1=8,E、F分别为AD和CC1的中点,O1为下底面正方形的中心。
(Ⅰ)证明:AF⊥平面FD1B1;
(Ⅱ)求异面直线EB与O1F所成角的余弦值;

(Ⅰ)证明见解析(Ⅱ)![]()
解析:
本题考查空间的线面关系,向量法及其运算。
(Ⅰ)证法一:如图建立空间直角坐标系。则D1(0,0,0)、O1(2,2,0)
B1(4,4,0)、E(2,0,8)、A(4,0,8)、B(4,4,8)、
F(0,4,4)。
![]() =(-4,4,-4),
=(-4,4,-4),![]() =(0,4,4),
=(0,4,4),
![]() =(-4,0,4)
=(-4,0,4)
![]() =0+16-16=0,
=0+16-16=0,![]() =16+0-16=0
=16+0-16=0
∴AF⊥平面FD1B1.
证法二:连结BF、DF,则BF是AF在面BC1上的射影,易证得BF⊥B1F,
DF是AF在面DC1上的射影,也易证得DF⊥D1F,所
以AF⊥平面FD1B1.
(Ⅱ)解法一:![]() =(2,4,0),
=(2,4,0),![]() =(-2,2,4)
=(-2,2,4)
设![]() 与
与![]() 的夹角为
的夹角为![]() ,则
,则
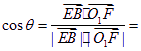
![]() =
=![]() ……
……
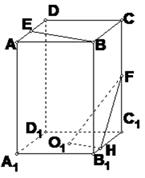
解法二:在B1C1上取点H,使B1H=1,连O1H和FH。
易证明O1H∥EB,则∠FO1H为异面直线EB与![]() F所成角。
F所成角。
又O1H=![]() BE=
BE=![]() ,HF=
,HF=![]() =5,
=5,
O1F=![]() =2
=2![]() ,
,
∴在△O1HF中,由余弦定理,得
cos∠FO1H=![]() =
=![]()

练习册系列答案
相关题目
已知长方体ABCD-A1B1C1D1,下列向量的数量积一定不为0的是( )


A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 已知长方体ABCD-A1B1C1D1中,AB=2,BC=4,AA1=4,点M是棱D1C1的中点.
已知长方体ABCD-A1B1C1D1中,AB=2,BC=4,AA1=4,点M是棱D1C1的中点. 已知长方体ABCD-A1B1C1D1中,DA=DD1=1,
已知长方体ABCD-A1B1C1D1中,DA=DD1=1, 已知长方体ABCD-A1B1C1D1中,M、N分别是BB1和BC的中点,AB=4,AD=2,
已知长方体ABCD-A1B1C1D1中,M、N分别是BB1和BC的中点,AB=4,AD=2, 如图,已知长方体ABCD-A1B1C1D1,AB=BC=1,BB1=2,连接B1C,过B点作B1C.
如图,已知长方体ABCD-A1B1C1D1,AB=BC=1,BB1=2,连接B1C,过B点作B1C.