题目内容
已知集合A={a,b,2},B={2,b2,2a},且A∩B=A∪B,则a=分析:利用集合交并运算的定义寻求A,B的关系是解决本题的关键.再根据集合相等确定未知数的等式关系,通过解方程组求解出所求的实数a值.注意元素互异性的应用.
解答:解:由A∩B=A∪B知A=B,又根据集合元素的互异性,
所以有
或
,解得
或
,
故a=0或
.
答案:0或
所以有
|
|
|
|
故a=0或
| 1 |
| 4 |
答案:0或
| 1 |
| 4 |
点评:本题考查学生等价转化的思想,集合相等的转化,集合中元素的互异性.考查学生列方程求解未知数的思想.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
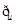 B)=R,则实数a的取值范围是 ( )
B)=R,则实数a的取值范围是 ( )