题目内容
(1)已知:等差数列{an}的首项a1,公差d,证明数列前n项和Sn=na1+
d;
(2)已知:等比数列{an}的首项a1,公比q,则证明数列前n项和Sn=
.
| n(n-1) |
| 2 |
(2)已知:等比数列{an}的首项a1,公比q,则证明数列前n项和Sn=
|
分析:(1)由于 sn=a1+(a1+d)+(a1+2d)+…+[a1+(n-1)d],且 sn=an+(an-d)+(an-2d)+…+[an-(n-1)d],两式相加即可证得结论.
(2)当公比q=1时,等比数列{an}的所有项都等于a1,可得sn=na1.当公比q≠1时,由于sn=a1+a1q+a1q2+…+a1qn-1,qsn=a1q+a1q2+a1q3+…+a1qn-1+a1 qn,错位相减可得(1-q)sn=a1-a1qn,从而证得结论成立.
(2)当公比q=1时,等比数列{an}的所有项都等于a1,可得sn=na1.当公比q≠1时,由于sn=a1+a1q+a1q2+…+a1qn-1,qsn=a1q+a1q2+a1q3+…+a1qn-1+a1 qn,错位相减可得(1-q)sn=a1-a1qn,从而证得结论成立.
解答:(1)证明:∵sn=a1+(a1+d)+(a1+2d)+…+[a1+(n-1)d],
sn=an+(an-d)+(an-2d)+…+[an-(n-1)d],
相加可得 2sn=n(a1+an),∴sn=
.
再把 an=a1+(n-1)d 代入可得 Sn=na1+
d.
(2)证明:当公比q=1时,等比数列{an}的所有项都等于a1,∴sn=na1.
当公比q≠1时,∵sn=a1+a1q+a1q2+…+a1qn-1,
qsn=a1q+a1q2+a1q3+…+a1qn-1+a1 qn,
错位相减可得(1-q)sn=a1-a1qn,
∴sn=
=
,
故Sn=
.
sn=an+(an-d)+(an-2d)+…+[an-(n-1)d],
相加可得 2sn=n(a1+an),∴sn=
| n(a1+an) |
| 2 |
再把 an=a1+(n-1)d 代入可得 Sn=na1+
| n(n-1) |
| 2 |
(2)证明:当公比q=1时,等比数列{an}的所有项都等于a1,∴sn=na1.
当公比q≠1时,∵sn=a1+a1q+a1q2+…+a1qn-1,
qsn=a1q+a1q2+a1q3+…+a1qn-1+a1 qn,
错位相减可得(1-q)sn=a1-a1qn,
∴sn=
| a 1 -a1 qn |
| 1-q |
| a1(1-qn) |
| 1-q |
故Sn=
|
点评:本题主要考查用倒序相加法等差数列前n项和公式,用错位相减法等比数列前n项和公式,属于中档题.

练习册系列答案
相关题目
已知一个等差数列共有2n+1项,其中奇数项之和为290,偶数项之和为261,则第n+1项为( )
| A、30 | B、29 | C、28 | D、27 |
 ;
;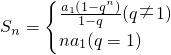 .
. ;
;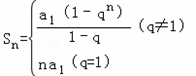 .
.