题目内容
(3分)(2011•重庆)已知a>0,b>0,a+b=2,则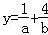 的最小值是( )
的最小值是( )
A.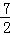 | B.4 | C.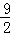 | D.5 |
C
解析试题分析:利用题设中的等式,把y的表达式转化成(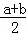 )(
)(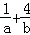 )展开后,利用基本不等式求得y的最小值.
)展开后,利用基本不等式求得y的最小值.
解:∵a+b=2,
∴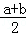 =1
=1
∴ =(
=(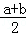 )(
)(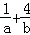 )=
)=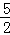 +
+ +
+ ≥
≥ +2=
+2=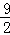 (当且仅当b=2a时等号成立)
(当且仅当b=2a时等号成立)
故选C
点评:本题主要考查了基本不等式求最值.注意把握好一定,二正,三相等的原则.

练习册系列答案
相关题目
在下列函数中,当x取正整数时,最小值为2的是
A.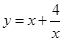 | B.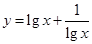 |
C.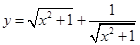 | D.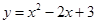 |
设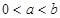 ,则下列不等式中正确的是( )
,则下列不等式中正确的是( )
A.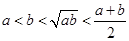 | B.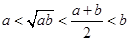 |
C.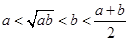 | D.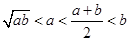 |
设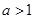 ,
,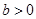 ,若
,若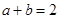 ,则
,则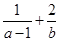 的最小值为
的最小值为
A.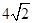 | B.6 | C.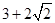 | D.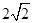 |
已知命题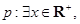 使得
使得 ;命题
;命题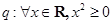 .则下列命题为真命题的是( )
.则下列命题为真命题的是( )
A.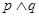 | B.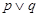 | C.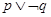 | D.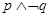 |
下列各函数中,最小值为2的是( ).
A.y=x+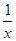 |
B.y=sin x+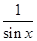 ,x∈ ,x∈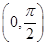 |
C.y=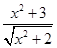 |
D.y=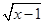 + +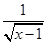 |
设 若
若 的最小值 ( )
的最小值 ( )
| A.2 |
B.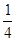 |
| C.4 |
| D.8 |
已知a>0,b>0,且2是2a与b的等差中项,则 的最小值为( )
的最小值为( )
A. | B. | C.2 | D.4 |
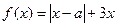 ,其中
,其中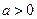 。
。 时,求不等式
时,求不等式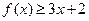 的解集;
的解集; 的解集为
的解集为 ,求a的值。
,求a的值。