题目内容
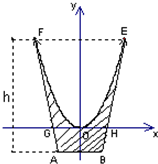 一个特殊模具容器横断面如图所示:内壁是抛物线y=
一个特殊模具容器横断面如图所示:内壁是抛物线y=| 1 |
| 2 |
| 1 |
| 2 |
(Ⅰ)求切线BE的方程和容器的高h;
(Ⅱ)求这个容器横断面的面积(阴影部分)
分析:(Ⅰ)欲求切线BE方程,只需求出切点E的坐标和切线斜率,因为EF=8厘米,所以可求E点的横坐标,代入抛物线方程就可求出E点的纵坐标,再根据切线的斜率是曲线在切点处的导数,通过求导,就可求出切线BE的斜率,得到BE的方程.
容器的高h等于直线AB与直线EF之间的距离,也即点B与点F的纵坐标之差的绝对值,由前面已知E点坐标,因为AB=3厘米,所以B点横坐标为
,又因为B点在直线BE上,代入直线BE方程,就可得到B点纵坐标,求出容器的高h.
(Ⅱ)有图知这个容器横断面的面积为梯形ABEF的面积,减去直线EF与抛物线y=
x2所围曲边梯形的面积,由(Ⅰ)可知梯形的上下底长和高,易求面积,而曲边梯形的面积即为函数y=8-
x2在区间[-4,4]的定积分,所以阴影面积可求.
容器的高h等于直线AB与直线EF之间的距离,也即点B与点F的纵坐标之差的绝对值,由前面已知E点坐标,因为AB=3厘米,所以B点横坐标为
| 3 |
| 2 |
(Ⅱ)有图知这个容器横断面的面积为梯形ABEF的面积,减去直线EF与抛物线y=
| 1 |
| 2 |
| 1 |
| 2 |
解答: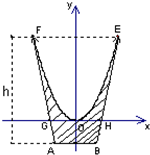 解:(Ⅰ)∵EF=8,且EF关于y轴对称,∴点E的横坐标为4,
解:(Ⅰ)∵EF=8,且EF关于y轴对称,∴点E的横坐标为4,
又∵点E在抛物线y=
x2上,∴点E的纵坐标是yE=8即E(4,8)
函数y=
x2的导数为y′=x
∵直线BE与抛物线y=
x2相切,E为切点,
∴直线BE的斜率k=y'|x=4=4
∴直线BE的方程是y-8=4(x-4)即y=4x-8
∵AB=3,且AB关于y轴对称,∴B的横坐标是xB=
,
又点B在直线y=4x-8上
∴点B的纵坐标是yB=4×
-8=-2
∴h=yE-yB=8-(-2)=10
即容器的高为10厘米
(Ⅱ)∵EF=8,E点的横坐标为4,∴F点的横坐标为-4.
S梯形ABEF=
=
=55
∵直线EF方程为y=8,
∴抛物线y=
x2与直线EF所围曲边图形面积S0=∫-44(8-
x2)dx=(8x-
x3)|-44=
∴容器横断面的面积S=S梯形ABEF-S0=55-
=
∴这个容器横断面的面积
平方厘米
 解:(Ⅰ)∵EF=8,且EF关于y轴对称,∴点E的横坐标为4,
解:(Ⅰ)∵EF=8,且EF关于y轴对称,∴点E的横坐标为4,又∵点E在抛物线y=
| 1 |
| 2 |
函数y=
| 1 |
| 2 |
∵直线BE与抛物线y=
| 1 |
| 2 |
∴直线BE的斜率k=y'|x=4=4
∴直线BE的方程是y-8=4(x-4)即y=4x-8
∵AB=3,且AB关于y轴对称,∴B的横坐标是xB=
| 3 |
| 2 |
又点B在直线y=4x-8上
∴点B的纵坐标是yB=4×
| 3 |
| 2 |
∴h=yE-yB=8-(-2)=10
即容器的高为10厘米
(Ⅱ)∵EF=8,E点的横坐标为4,∴F点的横坐标为-4.
S梯形ABEF=
| (AB+EF)•h |
| 2 |
| (3+8)×10 |
| 2 |
∵直线EF方程为y=8,
∴抛物线y=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 6 |
| 128 |
| 3 |
∴容器横断面的面积S=S梯形ABEF-S0=55-
| 128 |
| 3 |
| 37 |
| 3 |
∴这个容器横断面的面积
| 37 |
| 3 |
点评:本题主要考查了导数的几何意义,函数在某点处的切线方程的求法,定积分的几何意义,微积分基本定理及其应用

练习册系列答案
相关题目
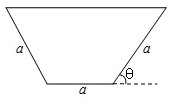 如图所示的等腰梯形是一个简易水槽的横断面,已知水槽的最大流量与横断面的面积成正比,比例系数为k(k>0).
如图所示的等腰梯形是一个简易水槽的横断面,已知水槽的最大流量与横断面的面积成正比,比例系数为k(k>0).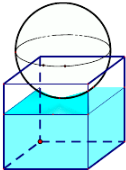 如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器注水,当球面恰好接触水面时测得水深为6cm,如不计容器的厚度,则球的体积为( )
如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器注水,当球面恰好接触水面时测得水深为6cm,如不计容器的厚度,则球的体积为( )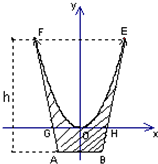 一个特殊模具容器横断面如图所示:内壁是抛物线
一个特殊模具容器横断面如图所示:内壁是抛物线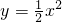 的一部分,外壁是等腰梯形ABEF的两腰AF、BE及底AB围成.已知EF=8厘米,AB=3厘米,点O到EF的距离是8厘米,BE所在直线与抛物线
的一部分,外壁是等腰梯形ABEF的两腰AF、BE及底AB围成.已知EF=8厘米,AB=3厘米,点O到EF的距离是8厘米,BE所在直线与抛物线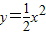 的一部分,外壁是等腰梯形ABEF的两腰AF、BE及底AB围成.已知EF=8厘米,AB=3厘米,点O到EF的距离是8厘米,BE所在直线与抛物线
的一部分,外壁是等腰梯形ABEF的两腰AF、BE及底AB围成.已知EF=8厘米,AB=3厘米,点O到EF的距离是8厘米,BE所在直线与抛物线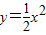 相切于点E.
相切于点E.