Question

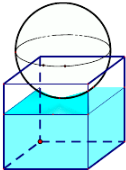如图，有一个水平放置的透明无盖的正方体容器，容器高8cm，将一个球放在容器口，再向容器注水，当球面恰好接触水面时测得水深为6cm，如不计容器的厚度，则球的体积为（　　）

• A．

  500π

  3

  cm3
• B．

  866π

  3

  cm3
• C．

  1372π

  3

  cm3
• D．

  2048π

  3

  cm3

Answer 1

分析：设正方体上底面所在平面截球得小圆M，可得圆心M为正方体上底面正方形的中心．设球的半径为R，根据题意得球心到上底面的距离等于（R-2）cm，而圆M的半径为4，由球的截面圆性质建立关于R的方程并解出R=5，用球的体积公式即可算出该球的体积．

解答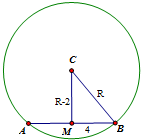：解：设正方体上底面所在平面截球得小圆M，
则圆心M为正方体上底面正方形的中心．如图．
设球的半径为R，根据题意得球心到上底面的距离等于（R-2）cm，而圆M的半径为4，由球的截面圆性质，得R²=（R-2）²+4²，
解出R=5，
∴根据球的体积公式，该球的体积V=

4π

3

R3=

4π

3

×53=

500π

3

cm3．
故选A．

点评：本题给出球与正方体相切的问题，求球的体积，着重考查了正方体的性质、球的截面圆性质和球的体积公式等知识，属于中档题．