题目内容
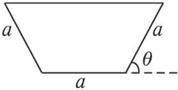
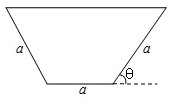 如图所示的等腰梯形是一个简易水槽的横断面,已知水槽的最大流量与横断面的面积成正比,比例系数为k(k>0).
如图所示的等腰梯形是一个简易水槽的横断面,已知水槽的最大流量与横断面的面积成正比,比例系数为k(k>0).(Ⅰ)试将水槽的最大流量表示成关于θ函数f(θ);
(Ⅱ)求当θ多大时,水槽的最大流量最大.
分析:(1)设水槽的截面面积为S,则S=
[a+(a+2acosθ)]•asinθ=a2sinθ(1+cosθ),由此能将水槽的最大流量表示成关于θ函数f(θ).
(2)因为f'(θ)=a2k(2cos2θ+cosθ-1),令f'(θ)=0,则2cos2θ+cosθ-1=0,解得cosθ=
或cosθ=-1.由此能求出当θ=
时,水槽的流量最大.
| 1 |
| 2 |
(2)因为f'(θ)=a2k(2cos2θ+cosθ-1),令f'(θ)=0,则2cos2θ+cosθ-1=0,解得cosθ=
| 1 |
| 2 |
| π |
| 3 |
解答:解:(1)设水槽的截面面积为S,
则S=
[a+(a+2acosθ)]•asinθ=a2sinθ(1+cosθ)
则f(θ)=kS=a2ksinθ(1+cosθ),θ∈(0,
).
(2)因为f'(θ)=a2k(2cos2θ+cosθ-1),
令f'(θ)=0,
则2cos2θ+cosθ-1=0,
解得cosθ=
或cosθ=-1.
由于0<θ<
,
得cosθ≠-1,
所以cosθ=
,
此时θ=
因为0<θ<
时,
f'(θ)>0;
<θ<
时,
f'(θ)<0;
所以,当θ=
时,水槽的流量最大.
则S=
| 1 |
| 2 |
则f(θ)=kS=a2ksinθ(1+cosθ),θ∈(0,
| π |
| 2 |
(2)因为f'(θ)=a2k(2cos2θ+cosθ-1),
令f'(θ)=0,
则2cos2θ+cosθ-1=0,
解得cosθ=
| 1 |
| 2 |
由于0<θ<
| π |
| 2 |
得cosθ≠-1,
所以cosθ=
| 1 |
| 2 |
此时θ=
| π |
| 3 |
因为0<θ<
| π |
| 3 |
f'(θ)>0;
| π |
| 3 |
| π |
| 2 |
f'(θ)<0;
所以,当θ=
| π |
| 3 |
点评:本题考查函数问题的实际应用,解题时要认真审题,寻找数量间的等量关系,合理地建立函数关系进行求解.

练习册系列答案
相关题目
 如图所示的等腰梯形是一个简易水槽的横断面,已知水槽的最大流量与横断面的面积成正比,比例系数为k(k>0).当θ=
如图所示的等腰梯形是一个简易水槽的横断面,已知水槽的最大流量与横断面的面积成正比,比例系数为k(k>0).当θ=
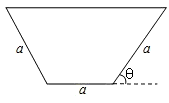 如图所示的等腰梯形是一个简易水槽的横断面,已知水槽的最大流量与横断面的面积成正比,比例系数为k(k>0).
如图所示的等腰梯形是一个简易水槽的横断面,已知水槽的最大流量与横断面的面积成正比,比例系数为k(k>0).