题目内容
如右图所示,等腰三角形△ABC的底边AB=6,高CD=3,
点E是线段BD上异于B、D的动点,点F在BC边上,且EF⊥AB,现沿EF将△BEF折起到△PEF的位置,使PE⊥AE,记BE=x,V(x)表示四棱锥P-ACEF的体积.
(1)求V(x)的表达式;
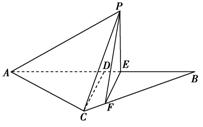 (2)当x为何值时,V(x)取得最大值?
(2)当x为何值时,V(x)取得最大值?
(3)当V(x)取得最大值时,求异面直线AC与PF所成角的余弦值
【答案】
(1)由折起的过程可知,PE⊥平面ABC,
SΔABC=9,S△BEF=·S△BDC=x2,
V(x)=x(0<x<3).
(2)V′(x)=,所以x∈(0,6)时,V′(x)>0 ,V(x)单调递增;6<x<3时V′(x)<0 ,V(x)单调递减;因此x=6时,V(x)取得最大值12;
(3)过F作MF∥AC交AD于M,则
===,MB=2BE=12,PM=6,
MF=BF=PF=BC==,
在△PFM中, cos∠PFM==,
∴异面直线AC与PF所成角的余弦值为.
【解析】略

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
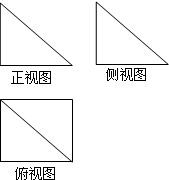 一个几何体的三视图如右图所示,其中正视图和侧视图是腰长为6的两个全等的等腰直角三角形.请画出该几何体的直观图,并求出它的体积.
一个几何体的三视图如右图所示,其中正视图和侧视图是腰长为6的两个全等的等腰直角三角形.请画出该几何体的直观图,并求出它的体积.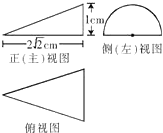 一个几何体的三视图及其尺寸如右图所示,其中正(主)视图是直角三角形,侧(左)视图是半圆,俯视图是等腰三角形,则这个几何体的表现积是
一个几何体的三视图及其尺寸如右图所示,其中正(主)视图是直角三角形,侧(左)视图是半圆,俯视图是等腰三角形,则这个几何体的表现积是 一个几何体的三视图如右图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,若要拼成一个棱长为1的正方体,则需要这样的几何体
一个几何体的三视图如右图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,若要拼成一个棱长为1的正方体,则需要这样的几何体