题目内容
已知数列{an}的各项均为正数,观察如图的程序框图,若k=5,k=10时,分别有S= 和S=
和S=
(1)试求数列{an}的通项;
(2)令bn=n•2a(n∈N+),求数列{bn}的前n项和Tn的值.

【答案】分析:(1)数列{an}的各项均为正数,观察如图的程序框图,主要循环条件i>k,求和M= ,求出S,讨论d与0的关系,从而求数列{an}的通项;
,求出S,讨论d与0的关系,从而求数列{an}的通项;
(2)由(1)可得:bn=n•22n-1,数列{bn}的前n项和Tn的值,利用错位相减法求出Tn,从而进行求解;
解答:解:(1)由框图可知S= +
+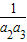 +…+
+…+ ,
,
∵{an}是等差数列,设公差为d,
若d=0,则当k=5时,S=5× =
= 可得a1=
可得a1= ,
,
当k=10时,S=10× =
= 可得a1=
可得a1=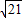 ,显然不成立,故舍去,
,显然不成立,故舍去,
∴d≠0,∴ =
= (
( -
- ),
),
所以,S= =
= (
( )
)
由题意可知,k=5时,S= ,k=10时,S=
,k=10时,S= ,
,
 ⇒
⇒ ,
,
故an=2n-1;
(2)由(1)可得:bn=n•22n-1,
∴Tn=1•2+2•23+3•25+…+(n-1)•22n-3+n•22n-1①,
又22•Tn=1•23+2•25+…+(n-1)22n-1+n•22n+1,②
①-②得,
-3Tn=2+23+25+…+22n-1-n•22n+1= =
=
∴Tn= (1-4n)+
(1-4n)+ 即Tn=
即Tn= ;
;
点评:根据流程图计算运行结果是算法这一模块的重要题型,处理的步骤一般为:分析流程图,从流程图中即要分析出计算的类型,又要分析出参与计算的数据建立数学模型,根据第一步分析的结果,选择恰当的数学模型解模.算法和程序框图是新课标新增的内容,在近两年的新课标地区高考都考查到了,是一道中档题;
 ,求出S,讨论d与0的关系,从而求数列{an}的通项;
,求出S,讨论d与0的关系,从而求数列{an}的通项;(2)由(1)可得:bn=n•22n-1,数列{bn}的前n项和Tn的值,利用错位相减法求出Tn,从而进行求解;
解答:解:(1)由框图可知S=
 +
+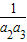 +…+
+…+ ,
,∵{an}是等差数列,设公差为d,
若d=0,则当k=5时,S=5×
 =
= 可得a1=
可得a1= ,
,当k=10时,S=10×
 =
= 可得a1=
可得a1=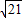 ,显然不成立,故舍去,
,显然不成立,故舍去,∴d≠0,∴
 =
= (
( -
- ),
),所以,S=
 =
= (
( )
)由题意可知,k=5时,S=
 ,k=10时,S=
,k=10时,S= ,
, ⇒
⇒ ,
,故an=2n-1;
(2)由(1)可得:bn=n•22n-1,
∴Tn=1•2+2•23+3•25+…+(n-1)•22n-3+n•22n-1①,
又22•Tn=1•23+2•25+…+(n-1)22n-1+n•22n+1,②
①-②得,
-3Tn=2+23+25+…+22n-1-n•22n+1=
 =
=
∴Tn=
 (1-4n)+
(1-4n)+ 即Tn=
即Tn= ;
;点评:根据流程图计算运行结果是算法这一模块的重要题型,处理的步骤一般为:分析流程图,从流程图中即要分析出计算的类型,又要分析出参与计算的数据建立数学模型,根据第一步分析的结果,选择恰当的数学模型解模.算法和程序框图是新课标新增的内容,在近两年的新课标地区高考都考查到了,是一道中档题;

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
 ,则下列各数是否为数列中的项?如果是,是第几项?如果不是,为什么?(1)
,则下列各数是否为数列中的项?如果是,是第几项?如果不是,为什么?(1) (2)
(2)
 ,则下列各数是否为数列中的项?如果是,是第几项?如果不是,为什么?(1)
,则下列各数是否为数列中的项?如果是,是第几项?如果不是,为什么?(1) (2)
(2)