题目内容

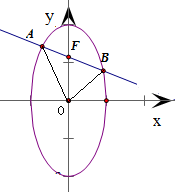
设A（x1，y1），B（x2，y2）是椭圆
y2
a2
+
x2
b2
=1(a＞b＞0)上的两点，已知O为坐标原点，椭圆的离心率e=
3
2
，短轴长为2，且
m
=(
x1
b
，
y1
a
)，
n
=(
x2
b
，
y2
a
)，若
m
•
n
=0．
（Ⅰ）求椭圆的方程；
（Ⅱ）若直线AB过椭圆的焦点F（0，c）（c为半焦距），求△AOB的面积．
分析：（1）根据题意，可得b=1且
a2-b2
a
=
3
2
，解出a=2，由此即可得到该椭圆的方程；

（2）由（1）得焦点F（0，
3
），设AB的方程为y=kx+
3
，与椭圆方程联解并消去y，得（k2+4）x2+2
3
kx-1=0，由根与系数的关系得x1+x2、x1x2关于k的表达式．由
m
•
n
=0，利用向量数量积的运算性质得到关于k的方程，解出k=±
2
，代入前面式子得x1+x2=?
2
6
6
，x1x2=-
1
6
，从而算出|x1-x2|=
2
3
3
，由此代入△AOB面积公式，即可得到所求△AOB的面积．
解答：解：（1）∵短轴长为2b=2，∴b=1
又∵椭圆的离心率e=
c
a
=
a2-b2
a
=
3
2


∴解得a=2，所以椭圆的方程为
y2
4
+x2=1（5分）
（2）由（1）得c=
a2-b2
=
3
，可得F（0，
3
）
由题意知直线AB的斜率存在，
设直线AB的方程为y=kx+
3
，与椭圆方程联解得
y=kx+
3
y2
4
+x2=1

消去y，得(k2+4)x2+2
3
kx-1=0
∴x1+x2=
-2
3
k
k2+4
，x1x2=
-1
k2+4
（7分）
∵
m
•
n
=0，
∴
x1x2
b2
+
y1y2
a2
=x1x2+
1
4
(kx1+
3
)(kx2+
3
)=(1+
k2
4
)x1x2+
3
k
4
(x1+x2)+
3
4

=
k2+4
4
(-
1
k2+4
)+
3
k
4
•
-2
3
k
k2+4
+
3
4
=0，解之得k=±
2
（10分）
∴x1+x2=
-2
3
k
k2+4
=?
2
6
6
，x1x2=
-1
k2+4
=-
1
6
，
由此可得|x1-x2|=
(x1+x2)2-4x1x2
=
(
2
6
6
)2-4(-
1
6
)
=
2
3
3

∴△AOB的面积为S△AOB=
1
2
|OF|•|x1-x2|=
3
2
•
2
3
3
=1．（13分）
点评：本题给出椭圆的短轴长和离心率，求椭圆的方程并依此求△AOB的面积．着重考查了椭圆的标准方程、直线与圆锥曲线的位置关系和坐标系中三角形面积求法等知识，属于中档题．
练习册系列答案
相关题目
已知抛物线C：x2=4y的焦点为F，直线l过点F交抛物线C于A、B两点．
（Ⅰ）设A（x1，y1），B（x2，y2），求
1
y1
+
1
y2
的取值范围；
（Ⅱ）是否存在定点Q，使得无论AB怎样运动都有∠AQF=∠BQF？证明你的结论．
设A（x1，y1），B（x2，y2）是函数f(x)=
1
2
+log2
x
1-x
的图象上两点，且
OM
=
1
2
(
OA
+
OB
)，O为坐标原点，已知点M的横坐标为
1
2
．
（Ⅰ）求证：点M的纵坐标为定值；
（Ⅱ）定义定义Sn=
n-1
i=1
f(
i
n
)=f(
1
n
)+f(
2
n
)+…+f(
n-1
n
)，其中n∈N*且n≥2，求S2011；
（Ⅲ）对于（Ⅱ）中的Sn，设an=
1
2Sn+1
(n∈N*)．若对于任意n∈N*，不等式kan3-3an2+1＞0恒成立，试求实数k的取值范围．
设A（x1，y1），B（x2，y2）是函数f（x）=
1
2
+log2
x
1-x
图象上任意两点，且
OM
=
1
2
（
OA
+
OB
），已知点M的横坐标为
1
2
，且有Sn=f（
1
n
）+f（
2
n
）+…+f（
n-1
n
），其中n∈N*且n≥2，
（1）求点M的纵坐标值；
（2）求s2，s3，s4及Sn；
（3）已知an=
1
(Sn+1)(Sn+1+1)
，其中n∈N*，且Tn为数列{an}的前n项和，若Tn≤λ（Sn+1+1）对一切n∈N*都成立，试求λ的最小正整数值．
设A（x1，y1）、B（x2，y2）、C（x3，y3）是抛物线y=x2上的三个动点，其中x3＞x2≥0，△ABC是以B为直角顶点的等腰直角三角形．
（1）求证：直线BC的斜率等于x2+x3，也等于
x2-x1x3-x2
；
（2）求A、C两点之间距离的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网