��Ŀ����
����Ŀ������������ҵ��Ĵ�һ������һ�����˲ݴ�һ��ͬ��Բ����һλ��ѧ��ʦһ�����Ϊ��й�����һ����Ϊ����2017������Ŀ����������⣺��OΪ����ԭ�㣬ֱ��l��ԲC1��x2+y2=1��������ԲC2��x2+y2=r2��r��1���ཻ��A��B����ͬ�㣬��֪![]() E��x1��y1����F��x2��y2���ֱ���ԲC1��ԲC2�ϵĵ㣮
E��x1��y1����F��x2��y2���ֱ���ԲC1��ԲC2�ϵĵ㣮
��1����r��ֵ��
��2������OEF��������ֵ��
��3������OEF�����ԲԲ��P��ԲC1�ϣ���֪��D��3��0������|DE|2+|DF|2��ȡֵ��Χ��
���𰸡���1��r=2����2��1����3��[23��6![]() ��23+6
��23+6![]() ].
].
�������������������1��ֱ��l��ԲC1��x2+y2=1���е��е�P����AB���е㣬���ù��ɶ������ɵ�r��ֵ����2����OE��OFʱ����OEF���ȡ���ֵ����3����OEF�����ԲԲ��P��ԲC1�ϣ�����OEF�����Բ��C2���У�����EOP=60����������P��cos����sin��������F��2cos����2sin������E��cos����+60�㣩��sin����+60����������ϵ�D��3��0��������������������Ǻ��������|DE|2+|DF|2��ȡֵ��Χ��
���������
��1����ͼ��ʾ��ֱ��l��ԲC1��x2+y2=1���е��е�P����AB���е㣬
��OP��AB��AB=2AP=2![]() �����r=2��
�����r=2��
��2����OEF�����S=![]() |OE|��|OF|sin��EOF��
|OE|��|OF|sin��EOF��
�ʵ�OE��OFʱ����OEF��������ֵΪ��S=![]() |OE|��|OF|=
|OE|��|OF|=![]() ��1��2=1��
��1��2=1��
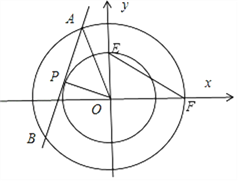
��3����OEF�����ԲԲ��P��ԲC1�ϣ�
��PE=PF=PO=1��
����OEF�����Բ��C2���У��ҡ�EOP=60����
������P��cos����sin��������F��2cos����2sin������E��cos����+60������sin����+60��������
�ߵ�D��3��0����
��![]() =��cos����+60������3��sin����+60��������
=��cos����+60������3��sin����+60��������![]() =��2cos����3��2sin������
=��2cos����3��2sin������
|DE|2+|DF|2=[cos����+60������3]2+sin2����+60����+��2cos����3��2+��2sin����2
=23��15cos��+3![]() sin��
sin��
=6![]() sin����������+23������tan��=
sin����������+23������tan��=![]() ��
��
��|DE|2+|DF|2��ȡֵ��ΧΪ[23��6![]() ��23+6
��23+6![]() ]
]

����Ŀ��Ϊ��Ӧ�����롰��ƶ���ᡱ�ĺ��٣�ij��λָ��һƶ����ͨ����ֲ�ϸ�������߾�������.�ϸ����Ի����¶�Ҫ��ϸߣ����������ľ��飬�����¶ȵ����ߣ�����������������������.�±�������2018����ֲ��һ�������ϸ����ڲ�ͬ�¶�ʱ6��������������
�¶� | 21 | 23 | 24 | 27 | 29 | 32 |
������ | 6 | 11 | 20 | 27 | 57 | 77 |
�����㣺![]() ��
��![]() ��
��![]() ��
��![]() .
.
����![]() �ֱ�Ϊ���������е��¶Ⱥ�����������
�ֱ�Ϊ���������е��¶Ⱥ�����������![]() ��
��
(1)![]() ��
��![]() �Ƿ��н�ǿ�����������? ��������ϵ��
�Ƿ��н�ǿ�����������? ��������ϵ��![]() (��ȷ��
(��ȷ��![]() )˵��.
)˵��.
(2)����![]() ����
����![]() �Ļع鷽��
�Ļع鷽��![]() (
(![]() ��
��![]() ����ȷ��
����ȷ��![]() )��
)��
(3)��(2)�е����Իع�ģ��Ԥ���¶�Ϊ![]() ʱ�����ϸ�����������(���ȡ����)��
ʱ�����ϸ�����������(���ȡ����)��
��������һ������![]() ��
��![]() ��������
��������![]() ��
��
���������ϵ��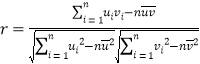 ��ͨ������µ�
��ͨ������µ�![]() ����0.8ʱ����Ϊ��
����0.8ʱ����Ϊ��
�������к�ǿ�������������
����ع�ֱ��![]() ��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ��
��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ��
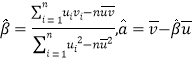 ��
��