题目内容
(2013•东城区一模)已知F1(-c,0),F2(c,0)分别是双曲线C1:
-
=1(a>0,b>0)的两个焦点,双曲线C1和圆C2:x2+y2=c2的一个交点为P,且2∠PF1F2=∠PF2F1,那么双曲线C1的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
分析:如图所示,利用圆的性质可得∠F1PF2=90°,再利用2∠PF1F2=∠PF2F1,得到∠PF1F2=30°.利用直角三角形的边角关系即可得到|PF2|=c,|PF1|=
c.再利用双曲线的定义及离心率的计算公式即可得出.
| 3 |
解答:解:如图所示,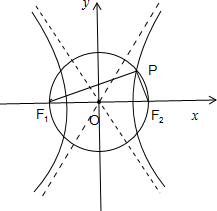
由题意可得∠F1PF2=90°,
又2∠PF1F2=∠PF2F1,∴∠PF1F2=30°.
∴|PF2|=c,|PF1|=
c.
由双曲线的定义可得:|PF1|-|PF2|=2a,
∴
c-c=2a,
解得
=
=
+1.
故选D.

由题意可得∠F1PF2=90°,
又2∠PF1F2=∠PF2F1,∴∠PF1F2=30°.
∴|PF2|=c,|PF1|=
| 3 |
由双曲线的定义可得:|PF1|-|PF2|=2a,
∴
| 3 |
解得
| c |
| a |
| 2 | ||
|
| 3 |
故选D.
点评:熟练掌握圆的性质、直角三角形的边角关系、双曲线的定义、离心率的计算公式是解题的关键.

练习册系列答案
相关题目
 (2013•东城区一模)数列{an}的各项排成如图所示的三角形形状,其中每一行比上一行增加两项,若
(2013•东城区一模)数列{an}的各项排成如图所示的三角形形状,其中每一行比上一行增加两项,若