题目内容
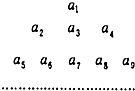 (2013•东城区一模)数列{an}的各项排成如图所示的三角形形状,其中每一行比上一行增加两项,若an=an(a≠0),则位于第10行的第8列的项等于
(2013•东城区一模)数列{an}的各项排成如图所示的三角形形状,其中每一行比上一行增加两项,若an=an(a≠0),则位于第10行的第8列的项等于a89
a89
,a2013在图中位于第45行的第77列
第45行的第77列
.(填第几行的第几列)分析:①由于每行的所有数的个数形成等差数列,故可得到前9行的数的个数,从而得出答案;
②由①可知前k行所有ai的个数为b1+b2+…bk=1+3+…(2k-1)=k2.解出(k-1)2≤2013即可得出答案.
②由①可知前k行所有ai的个数为b1+b2+…bk=1+3+…(2k-1)=k2.解出(k-1)2≤2013即可得出答案.
解答:解:①设每行的数的个数为数列{bn},则此数列为首项为1,公差为2的等差数列,∴bn=1+(n-1)×2=2n-1.
于是前9行所有an的个数为b1+b2+…+b9=
=81.
∴位于第10行的第8列的项等于a81+8=a89=a89.
②由①可知:前k行所有ai的个数为b1+b2+…bk=1+3+…(2k-1)=k2.
由(k-1)2<2013,解得k<1+
,
而442<2013<452,∴k<1+44=45.
∴前44行的所有数ai的个数为442=1936.
而1936+77=2013,
∴a2013在图中位于第45行的第77 列.
故答案分别为a89,第45行的第77 列.
于是前9行所有an的个数为b1+b2+…+b9=
| 9(1+2×9-1) |
| 2 |
∴位于第10行的第8列的项等于a81+8=a89=a89.
②由①可知:前k行所有ai的个数为b1+b2+…bk=1+3+…(2k-1)=k2.
由(k-1)2<2013,解得k<1+
| 2013 |
而442<2013<452,∴k<1+44=45.
∴前44行的所有数ai的个数为442=1936.
而1936+77=2013,
∴a2013在图中位于第45行的第77 列.
故答案分别为a89,第45行的第77 列.
点评:正确理解每行的所有数的个数形成等差数列,利用等差数列的通项公式和前可知前k行所有ai的个数为b1+b2+…bk=1+3+…(2k-1)=k2是解题的关键.

练习册系列答案
相关题目