题目内容
有下列四种说法：
①“若am2＜bm2，则a＜b”的逆命题为真；
②“命题p∨q为真”是“命题p∧q为真”的必要不充分条件；
③命题“?x0∈R使得x2-x＞0”的否定是“?x∈R都有x2-x≤0”；
④若实数x，y∈[0，1]，则满足：x2+y2＜1的概率为
．
其中正确命题的个数是（ ）
①“若am2＜bm2，则a＜b”的逆命题为真；
②“命题p∨q为真”是“命题p∧q为真”的必要不充分条件；
③命题“?x0∈R使得x2-x＞0”的否定是“?x∈R都有x2-x≤0”；
④若实数x，y∈[0，1]，则满足：x2+y2＜1的概率为
| π |
| 4 |
其中正确命题的个数是（ ）
分析：①当m=0时，“若am2＜bm2，则a＜b”的逆命题不成立；
②“命题p∨q为真”是指命题p，q中至少有一个是真命题，“命题p∧q为真”是指p，q都是真命题；
③利用特称命题判断真假；
④实数x，y∈[0，1]的区域面积为1，x2+y2＜1的面积=
，由此判断真假．
②“命题p∨q为真”是指命题p，q中至少有一个是真命题，“命题p∧q为真”是指p，q都是真命题；
③利用特称命题判断真假；
④实数x，y∈[0，1]的区域面积为1，x2+y2＜1的面积=
| π |
| 4 |
解答：解：①“若am2＜bm2，则a＜b”的逆命题是“若a＜b，则am2＜bm2”，
∵当m=0时不成立，∴①是假命题；
②∵“命题p∨q为真”是指命题p，q中至少有一个是真命题，
“命题p∧q为真”是指p，q都是真命题，故②是真命题；
③∵命题“?x0∈R使得x2-x＞0”是特称命题，
∴它的否定是“?x∈R都有x2-x≤0”，故③是真命题；
④∵实数x，y∈[0，1]，∴区域面积为1，
x2+y2＜1的面积=
，
∴若实数x，y∈[0，1]，则满足：x2+y2＜1的概率为
．故④是真命题．
故选D．
∵当m=0时不成立，∴①是假命题；
②∵“命题p∨q为真”是指命题p，q中至少有一个是真命题，
“命题p∧q为真”是指p，q都是真命题，故②是真命题；
③∵命题“?x0∈R使得x2-x＞0”是特称命题，
∴它的否定是“?x∈R都有x2-x≤0”，故③是真命题；
④∵实数x，y∈[0，1]，∴区域面积为1，
x2+y2＜1的面积=
| π |
| 4 |
∴若实数x，y∈[0，1]，则满足：x2+y2＜1的概率为
| π |
| 4 |
故选D．
点评：本题考查命题的真假判断与应用，解题时要认真审题，注意不等式、复合命题、特称命题、几何概型等知识点的合理运用．
练习册系列答案
相关题目
,使得
”的否定是“
,都有
”；
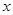服从正态分布
，
，则
；
图像关于直线
对称，且在区间
上是增函数；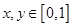
，则满足：
的概率为
。其中错误的个数是 （ ）