题目内容
有下列四种说法:
①函数y=
的值域是{y|y≥0};
②若集合A={x|x2-1=0},B={x|lg(x2-2)=lgx},则A∩B={-1};
③函数y=f(x)与函数y=f(-x)的图象关于直线x=0对称;
④已知A=B=R,对应法则f:x→y=
,则对应f是从A到B的映射.
其中你认为不正确的是
①函数y=
| 1-3x |
②若集合A={x|x2-1=0},B={x|lg(x2-2)=lgx},则A∩B={-1};
③函数y=f(x)与函数y=f(-x)的图象关于直线x=0对称;
④已知A=B=R,对应法则f:x→y=
| 1 |
| x+1 |
其中你认为不正确的是
①②④
①②④
.分析:①利用指数函数的单调性确定值域.②利用集合的基本运算计算.③利用函数之间的关系判断.④利用映射的定义判断.
解答:解:①因为3x>0,所以-3x<0,1-3x<1,所以0≤
<1,即函数y=
的值域是{y|y≥0},所以①错误.
②因为A={x|x2-1=0}={-1,1},在集合B中,由
,解得x=2,即B={2},所以A∩B=∅,所以②错误.
③函数y=f(x)与函数y=f(-x)的图象关于y轴对称,即关于直线x=0对称,所以③正确.
④当x=-1时,y=
分母等于0,所以函数无意义,即不满足映射的定义,所以④错误.
故不正确的是①②④.
故答案为:①②④.
| 1-3x |
| 1-3x |
②因为A={x|x2-1=0}={-1,1},在集合B中,由
|
③函数y=f(x)与函数y=f(-x)的图象关于y轴对称,即关于直线x=0对称,所以③正确.
④当x=-1时,y=
| 1 |
| x+1 |
故不正确的是①②④.
故答案为:①②④.
点评:本题主要考查命题的真假判断.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
 的值域是{y|y≥0};
的值域是{y|y≥0};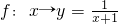 ,则对应f是从A到B的映射.
,则对应f是从A到B的映射.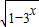 的值域是{y|y≥0};
的值域是{y|y≥0};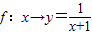 ,则对应f是从A到B的映射.
,则对应f是从A到B的映射.