题目内容
已知椭圆的两焦点是F1(0,-1),F2(0,1),离心率e=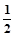
(1)求椭圆方程;
(2)若P在椭圆上,且|PF1|-|PF2|=1,求cos∠F1PF2
(1) 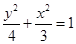 ; (2)
; (2)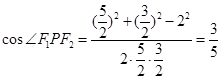
解析试题分析:(1)c=1 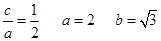 椭圆方程为
椭圆方程为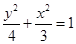
(2)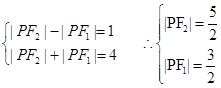

考点:本题主要考查椭圆的定义,几何性质。
点评:基础题,涉及椭圆的“焦点三角形”问题,往往要运用椭圆的定义,根据三角形的特征,运用勾股定理或余弦定理。

练习册系列答案
相关题目
题目内容
已知椭圆的两焦点是F1(0,-1),F2(0,1),离心率e=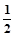
(1)求椭圆方程;
(2)若P在椭圆上,且|PF1|-|PF2|=1,求cos∠F1PF2
(1) 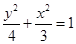 ; (2)
; (2)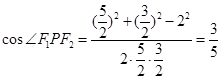
解析试题分析:(1)c=1 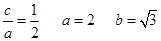 椭圆方程为
椭圆方程为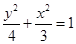
(2)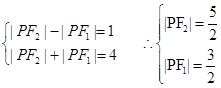

考点:本题主要考查椭圆的定义,几何性质。
点评:基础题,涉及椭圆的“焦点三角形”问题,往往要运用椭圆的定义,根据三角形的特征,运用勾股定理或余弦定理。
