题目内容
如图，A、B是椭圆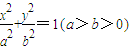
的长轴和短轴端点，点P在椭圆上，F、E是椭圆的左、右焦点，若EP∥AB，PF⊥OF，则该椭圆的离心率等于（ ）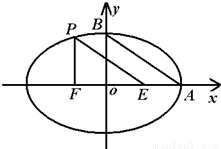
A．
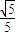
B．
C．
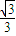
D．
【答案】分析：由PFE∽△BOA，知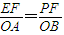
，所以a=
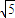c，由此能求出其离心率．
解答：解：如图，∵A、B是椭圆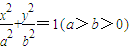
的长轴和短轴端点，
点P在椭圆上，F、E是椭圆的左、右焦点，EP∥AB，PF⊥OF，
∴△PFE∽△BOA，
∴
，
∴
，
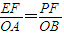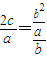∴b2=2bc，b=2c，
∴a2=b2+c2=5c2，a=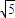
c，
∴e=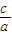
=
．
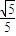故选A．
点评：本题考查椭圆的性质和应用，解题时要认真审题，仔细解答，注意合理地进行等价转化．
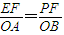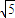，所以a=c，由此能求出其离心率．解答：解：如图，∵A、B是椭圆
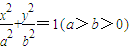的长轴和短轴端点，点P在椭圆上，F、E是椭圆的左、右焦点，EP∥AB，PF⊥OF，
∴△PFE∽△BOA，
∴
，∴
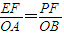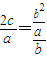，∴b2=2bc，b=2c，
∴a2=b2+c2=5c2，a=
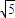c，∴e=
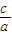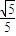=．故选A．
点评：本题考查椭圆的性质和应用，解题时要认真审题，仔细解答，注意合理地进行等价转化．
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
如图，A，B是椭圆
的左右顶点，M是椭圆上异于A，B的任意一点，若椭圆C的离心率为
，且右准线l的方程为x=4．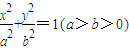
的长轴和短轴端点，点P在椭圆上，F、E是椭圆的左、右焦点，若EP∥AB，PF⊥OF，则该椭圆的离心率等于（ ）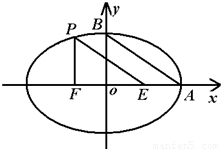
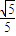
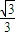
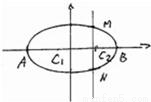
的左、右顶点，直线x=t（-2＜t＜2）交椭圆于M、N两点，经过A、M、N的圆的圆心为C1，经过B、M、N的圆的圆心为C2．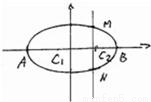
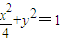的左、右顶点，直线x=t（-2＜t＜2）交椭圆于M、N两点，经过A、M、N的圆的圆心为C1，经过B、M、N的圆的圆心为C2．