题目内容
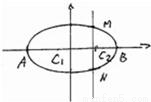
已知如图,A、B是椭圆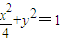 的左、右顶点,直线x=t(-2<t<2)交椭圆于M、N两点,经过A、M、N的圆的圆心为C1,经过B、M、N的圆的圆心为C2.
的左、右顶点,直线x=t(-2<t<2)交椭圆于M、N两点,经过A、M、N的圆的圆心为C1,经过B、M、N的圆的圆心为C2.(1)求证|C1C2|为定值;
(2)求圆C1与圆C2的面积之和的取值范围.
【答案】分析:(1)根据椭圆方程可求得A,B的坐标,把直线方程与椭圆方程联立求得M,N的坐标,设C1(x1,0),C2(x2,0),根据半径相等建立等式求得x1和x2的表达式,进而求得|C1C2|=x2-x1结果为常数.原式得证.
(2)依题意可分别表示出两个圆的半径,进而根据圆的面积公式求得S,进而二次函数的性质求得答案.
解答:解:(1)由题设A(-2,0),B(2,0),
由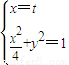 解出
解出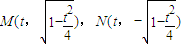 .
.
设C1(x1,0),C2(x2,0),由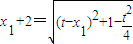 解出
解出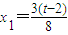 .
.
同理,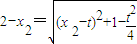 解出
解出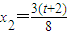 ,
,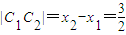 (定值).
(定值).
(2)两圆半径分别为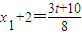 及
及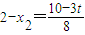 ,
,
两圆面积和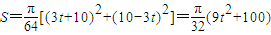 ,
,
因为-2<t<2,所以0≤t2<4,所以S的取值范围是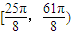 .
.
点评:本题主要考查了椭圆的应用.涉及了椭圆与圆的位置关系,圆的面积公式,点与点之间的距离公式.
(2)依题意可分别表示出两个圆的半径,进而根据圆的面积公式求得S,进而二次函数的性质求得答案.
解答:解:(1)由题设A(-2,0),B(2,0),
由
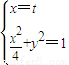 解出
解出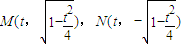 .
.设C1(x1,0),C2(x2,0),由
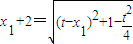 解出
解出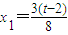 .
.同理,
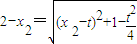 解出
解出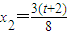 ,
,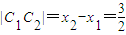 (定值).
(定值).(2)两圆半径分别为
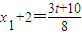 及
及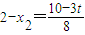 ,
,两圆面积和
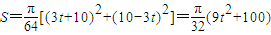 ,
,因为-2<t<2,所以0≤t2<4,所以S的取值范围是
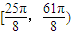 .
.点评:本题主要考查了椭圆的应用.涉及了椭圆与圆的位置关系,圆的面积公式,点与点之间的距离公式.

练习册系列答案
相关题目
如图,已知椭圆C的中心在原点O,焦点在 轴上,长轴长是短轴
轴上,长轴长是短轴
长的2倍,且经过点M .
平行于OM的直线
.
平行于OM的直线 在
在 轴上的截距为
轴上的截距为
 并交椭
并交椭
圆C于A、B两个不同点.
(1)求椭圆C的标准方程;
(2)求 的取值范围;
的取值范围;
|
 轴始终围成一个等腰三角形.
轴始终围成一个等腰三角形.

 (2013•浦东新区二模)(1)设椭圆C1:
(2013•浦东新区二模)(1)设椭圆C1: 如图,F1,F2为椭圆C:
如图,F1,F2为椭圆C:
 (其中
(其中 为一正实数)到实数集R上的映射过程:区间
为一正实数)到实数集R上的映射过程:区间 对应线段
对应线段 上的点
上的点 ,如图1;将线段
,如图1;将线段 的椭圆,使两端点
的椭圆,使两端点 、
、 恰好重合于椭圆的一个短轴端点,如图2 ;再将这个椭圆放在平面直角坐标系中,使其中心在坐标原点,长轴在
恰好重合于椭圆的一个短轴端点,如图2 ;再将这个椭圆放在平面直角坐标系中,使其中心在坐标原点,长轴在 轴上,已知此时点
轴上,已知此时点 ,如图3,在图形变化过程中,图1中线段
,如图3,在图形变化过程中,图1中线段 的长度对应于图3中的椭圆弧ADM的长度.图3中直线
的长度对应于图3中的椭圆弧ADM的长度.图3中直线 交于点
交于点 ,则与实数
,则与实数 ,记作
,记作 ,
,
 ;
②函数
;
②函数 是奇函数;③函数
是奇函数;③函数 上单调递增; ④.函数
上单调递增; ④.函数 对称;⑤函数
对称;⑤函数 时AM过椭圆的右焦点.其中所有的真命题是: ( )
时AM过椭圆的右焦点.其中所有的真命题是: ( )