题目内容
有甲、乙两个班级进行数学考试,按照大于或等于85分为优秀,85分以下为非优秀统计成绩后,得到如下 联表:
联表:
已知全部200人中随机抽取1人为优秀的概率为
(1)请完成上面 联表;
联表;
(2)根据列联表的数据,能否有 的把握认为“成绩与班级有关系”
的把握认为“成绩与班级有关系”
(3)从全部200人中有放回抽取3次,每次抽取一人,记被抽取的3人中优秀的人数为 ,若每次抽取得结果是相互独立的,求
,若每次抽取得结果是相互独立的,求 的分布列,期望
的分布列,期望 和方差
和方差
参考公式与参考数据如下:

 联表:
联表:| | 优秀 | 非优秀 | 合计 |
| 甲班 | 30 | | |
| 乙班 | | 50 | |
| 合计 | | | 200 |

(1)请完成上面
 联表;
联表;(2)根据列联表的数据,能否有
 的把握认为“成绩与班级有关系”
的把握认为“成绩与班级有关系”(3)从全部200人中有放回抽取3次,每次抽取一人,记被抽取的3人中优秀的人数为
 ,若每次抽取得结果是相互独立的,求
,若每次抽取得结果是相互独立的,求 的分布列,期望
的分布列,期望 和方差
和方差
参考公式与参考数据如下:


(1)
(2) ,有
,有 的把握
的把握
(3) ,
, ,
,
| | 优秀 | 非优秀 | 合计 |
| 甲班 | 30 | 70 | 100 |
| 乙班 | 50 | 50 | 100 |
| 合计 | 80 | 120 | 200 |
 ,有
,有 的把握
的把握(3)
 ,
, ,
,
试题分析:(1)根据题意,由于全部200人中随机抽取1人为优秀的概率为
 ,那么可知优秀的人数为80,那么可知不优秀的人数为120,那么可知得到列联表为:
,那么可知优秀的人数为80,那么可知不优秀的人数为120,那么可知得到列联表为:| | 优秀 | 非优秀 | 合计 |
| 甲班 | 30 | 70 | 100 |
| 乙班 | 50 | 50 | 100 |
| 合计 | 80 | 120 | 200 |
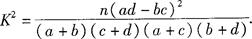 ,可知
,可知 ,有
,有 的把握认为“成绩与班级有关系”
的把握认为“成绩与班级有关系”(3)由于全部200人中有放回抽取3次,每次抽取一人,记被抽取的3人中优秀的人数为
 ,那么可知
,那么可知 ,
, ,
,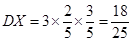 ,。
,。点评:主要是考查了独立性检验的思想的运用,以及二项分布的运用,属于中档题。

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目




 ,其中
,其中 )
)
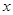 与身高
与身高 进行测量,得到数据(单位均为
进行测量,得到数据(单位均为 )作为样本如下表所示.
)作为样本如下表所示.
 ;
; ,试估计此人的身高;
,试估计此人的身高; ,
, ,
, ,
, )
) 位学生(关心与不关心的各一半),
位学生(关心与不关心的各一半),
 ℅的把握认为是否关心创卫活动与性别有关?
℅的把握认为是否关心创卫活动与性别有关?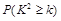

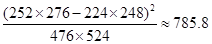
 ;
; 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量 .
. 的样本中数据分成6个组,制成一个频率分布表,若第一组至第六组的数据频率之比为2:3:4:6:4:1,且前三组数据的频数之和为27,则
的样本中数据分成6个组,制成一个频率分布表,若第一组至第六组的数据频率之比为2:3:4:6:4:1,且前三组数据的频数之和为27,则


 ,变量
,变量 增加一个单位时,则
增加一个单位时,则 平均增加
平均增加 个单位
个单位 