题目内容
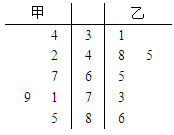
某校高三2班有48名学生进行了一场投篮测试,其中男生28人,女生20人.为了了解其投篮成绩,甲、乙两人分别对全班的学生进行编号(1~48号),并以不同的方法进行数据抽样,其中一人用的是系统抽样,另一人用的是分层抽样.若此次投篮考试的成绩大于或等于80分视为优秀,小于80分视为不优秀,以下是甲、乙两人分别抽取的样本数据:

(Ⅰ)从甲抽取的样本数据中任取两名同学的投篮成绩,记“抽到投篮成绩优秀”的人数为X,求X的分布列和数学期望;
(Ⅱ)请你根据乙抽取的样本数据完成下列2×2列联表,判断是否有95%以上的把握认为投篮成绩和性别有关?

(Ⅲ)判断甲、乙各用何种抽样方法,并根据(Ⅱ)的结论判断哪种抽样方法更优?说明理由.
下面的临界值表供参考:
(参考公式: ,其中
,其中 )
)

(Ⅰ)从甲抽取的样本数据中任取两名同学的投篮成绩,记“抽到投篮成绩优秀”的人数为X,求X的分布列和数学期望;
(Ⅱ)请你根据乙抽取的样本数据完成下列2×2列联表,判断是否有95%以上的把握认为投篮成绩和性别有关?

(Ⅲ)判断甲、乙各用何种抽样方法,并根据(Ⅱ)的结论判断哪种抽样方法更优?说明理由.
下面的临界值表供参考:
 | 0.15 | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
 ,其中
,其中 )
)(Ⅰ) 的分布列为
的分布列为
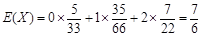 .
.
(Ⅱ)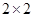 列联表:
列联表:
有95%以上的把握认为投篮成绩与性别有关.
(Ⅲ)甲用的是系统抽样,乙用的是分层抽样.投篮成绩与性别有关,并且从样本数据能看出投篮成绩与性别有明显差异,因此采用分层抽样方法比系统抽样方法更优.
 的分布列为
的分布列为 |  | 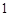 | 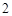 |
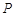 | 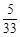 | 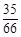 | 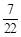 |
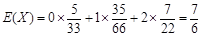 .
.(Ⅱ)
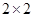 列联表:
列联表:| | 优秀 | 非优秀 | 合计 |
| 男 | 6 | 1 | 7 |
| 女 | 1 | 4 | 5 |
| 合计 | 7 | 5 | 12 |
(Ⅲ)甲用的是系统抽样,乙用的是分层抽样.投篮成绩与性别有关,并且从样本数据能看出投篮成绩与性别有明显差异,因此采用分层抽样方法比系统抽样方法更优.
试题分析:(Ⅰ)由“抽到投篮成绩优秀”的人数为X,其所有可能取值为
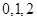 .
.计算可得相应概率,得到
 的分布列为
的分布列为 |  | 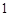 | 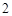 |
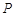 | 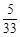 | 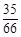 | 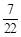 |
计算得到数学期望
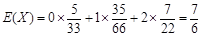 .
. (Ⅱ)由乙抽取的样本数据,得到
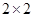 列联表,应用“卡方公式”计算“卡方”并与临界值表对照,得出结论.
列联表,应用“卡方公式”计算“卡方”并与临界值表对照,得出结论.(Ⅲ)对照系统抽样、分层抽样的定义.确定抽样方法,由(Ⅱ)的结论,并且从样本数据能看出投篮成绩与性别有明显差异,得到结论.
试题解析:(Ⅰ)由甲抽取的样本数据可知,投篮成绩优秀的有7人,投篮成绩不优秀的有5人.
X的所有可能取值为
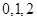 . 1分
. 1分所以
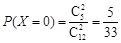 ,
,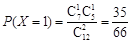 ,
,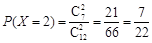 .4分
.4分故
 的分布列为
的分布列为 |  | 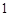 | 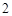 |
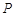 | 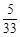 | 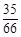 | 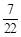 |
∴
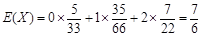 . 6分
. 6分(Ⅱ)设投篮成绩与性别无关,由乙抽取的样本数据,得
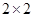 列联表如下:
列联表如下:| | 优秀 | 非优秀 | 合计 |
| 男 | 6 | 1 | 7 |
| 女 | 1 | 4 | 5 |
| 合计 | 7 | 5 | 12 |
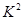 的观测值
的观测值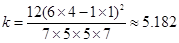
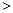 3.841, 9分
3.841, 9分所以有95%以上的把握认为投篮成绩与性别有关. 10分
(Ⅲ)甲用的是系统抽样,乙用的是分层抽样. 11分
由(Ⅱ)的结论知,投篮成绩与性别有关,并且从样本数据能看出投篮成绩与性别有明显差异,因此采用分层抽样方法比系统抽样方法更优. 13分

练习册系列答案
相关题目
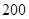 个样品,并对其寿命进行追踪调查,将结果列成频率分布表如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于
个样品,并对其寿命进行追踪调查,将结果列成频率分布表如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于 天的灯泡是优等品,寿命小于
天的灯泡是优等品,寿命小于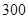 天的灯泡是次品,其余的灯泡是正品.
天的灯泡是次品,其余的灯泡是正品.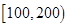
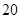
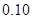
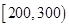
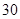
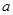
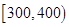
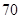
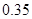
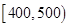
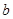
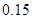
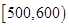
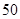
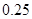
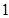
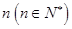 个,如果这
个,如果这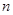 个灯泡的等级情况恰好与按三个等级分层抽样所得的结果相同,求
个灯泡的等级情况恰好与按三个等级分层抽样所得的结果相同,求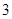 个进行使用,若以上述频率作为概率,用
个进行使用,若以上述频率作为概率,用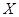 表示此人所购买的灯泡中次品的个数,求
表示此人所购买的灯泡中次品的个数,求 ,第2组
,第2组 ,第3组
,第3组 ,第4组
,第4组 ,第5组
,第5组 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.

 的值;
的值; 名男生和
名男生和




 列联表,并回答能否有90%的把握认为“学生周日上网时间与性别有关”?
列联表,并回答能否有90%的把握认为“学生周日上网时间与性别有关”? ,其中
,其中

 有关.
有关. 


 =0.56x+997.4 B.
=0.56x+997.4 B.  必过点
必过点 ;
; 且
且 ,则实数
,则实数
 ,使得
,使得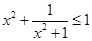 成立
成立 联表:
联表:
 的把握认为“成绩与班级有关系”
的把握认为“成绩与班级有关系” ,若每次抽取得结果是相互独立的,求
,若每次抽取得结果是相互独立的,求 和方差
和方差

