题目内容
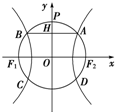 如图,双曲线
如图,双曲线| x2 |
| a2 |
| y2 |
| b2 |
| OH |
| 3 |
| HP |
(1)若双曲线的焦距为2,求双曲线的方程;
(2)求双曲线的离心率.
分析:(1)由|F1F2|=2可求得P(0,1),设H(0,m),由
=(3+2
)
可求得m,从而可求得A点的坐标,代入双曲线方程,得到a,b的关系式,与a2+b2=1联立即可求得双曲线的方程;
(2)设焦距为2c,则P(0,c),设H(0,n),同理可求得(
)2=3+2
?
=
=e2=4+2
,从而可得双曲线的离心率.
| OH |
| 3 |
| HP |
(2)设焦距为2c,则P(0,c),设H(0,n),同理可求得(
| b |
| a |
| 3 |
| a2+b2 |
| a2 |
| c2 |
| a2 |
| 3 |
解答:解:(1)由|F1F2|=2得圆O的半径为1,故P(0,1),设H(0,m).
∵
=(3+2
)
=(3+2
)(0,1-m),
∴m=(3+2
)(1-m),解得m=
,
故A(x,
),由|OA|=1得x=
,
∴A(
,
).
∵点A(
,
)在双曲线上,
∴
-
=1,
又∵焦距为2,
∴a2+b2=1,解得a2=1-
,b2=
,
故双曲线的方程为
-
=1.
(2)设焦距为2c,则P(0,c),设H(0,n).
∵
=(3+2
)
=(3+2
)(0,c-n),
∴n=(3+2
)(c-n),解得n=
c,
即H(0,
c).
由A(x0,
c)在圆上得x0=
c,
∴A(
c,
c),
∴将A(
c,
c)代入双曲线方程得
-
=1,
又∵a2+b2=c2,化简得3a4+6a2b2-b4=0,
即(
)4-6(
)2-3=0,
∴(
)2=3+2
,
∴e2=
=1+
=4+2
,
故双曲线的离心率为e=
+1.
∵
| OH |
| 3 |
| HP |
| 3 |
∴m=(3+2
| 3 |
| ||
| 2 |
故A(x,
| ||
| 2 |
| 1 |
| 2 |
∴A(
| 1 |
| 2 |
| ||
| 2 |
∵点A(
| 1 |
| 2 |
| ||
| 2 |
∴
| 1 |
| 4a2 |
| 3 |
| 4b2 |
又∵焦距为2,
∴a2+b2=1,解得a2=1-
| ||
| 2 |
| ||
| 2 |
故双曲线的方程为
| x2 | ||||
1-
|
| y2 | ||||
|
(2)设焦距为2c,则P(0,c),设H(0,n).
∵
| OH |
| 3 |
| HP |
| 3 |
∴n=(3+2
| 3 |
| ||
| 2 |
即H(0,
| ||
| 2 |
由A(x0,
| ||
| 2 |
| 1 |
| 2 |
∴A(
| 1 |
| 2 |
| ||
| 2 |
∴将A(
| 1 |
| 2 |
| ||
| 2 |
| c2 |
| 4a2 |
| 3c2 |
| 4b2 |
又∵a2+b2=c2,化简得3a4+6a2b2-b4=0,
即(
| b |
| a |
| b |
| a |
∴(
| b |
| a |
| 3 |
∴e2=
| c2 |
| a2 |
| b2 |
| a2 |
| 3 |
故双曲线的离心率为e=
| 3 |
点评:本题考查双曲线的标准方程与离心率,考查向量的坐标运算,考查方程思想与综合分析与运算能力,属于难题.

练习册系列答案
 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
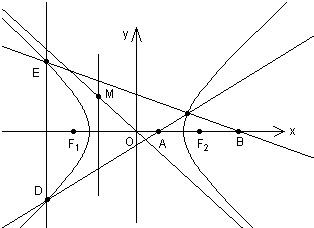 如图,双曲线
如图,双曲线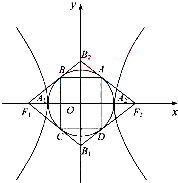 (2012•湖北)如图,双曲线
(2012•湖北)如图,双曲线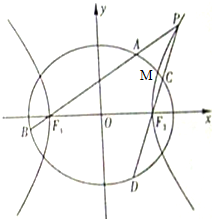 (2011•天津模拟)如图,椭圆
(2011•天津模拟)如图,椭圆 如图,双曲线C:
如图,双曲线C: