题目内容
 如图,双曲线C:
如图,双曲线C:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
| OP1 |
| OP2 |
| P2P |
| PP1 |
(1)若△P1OP2的面积为6,求t的值;
(2)t=5时,求a最大时双曲线C的方程.
分析:(1)依题意,由e=
=
可求得b=
a,设双曲线C:
-
=1(a>0,b>0)的渐近线l1:y=
x的倾斜角为θ,可求得tanθ=
,tan∠P1OP2=tan2θ=
,继而可求得cos2θ=
,sin2θ=
,由
•
=t,S△P1OP2=6即可求得t.
(2)t=5时,可求得|
|•|
|=13,利用余弦定理可求得|P1P2|,再利用基本不等式可求得|P1P2|≥16,最后利用S△P1OP2即可求得a最大时的值,从而可求得此时双曲线C的方程.
| c |
| a |
| ||
| 3 |
| 2 |
| 3 |
| x2 |
| a2 |
| y2 |
| b2 |
| b |
| a |
| 2 |
| 3 |
| 12 |
| 5 |
| 5 |
| 13 |
| 12 |
| 13 |
| OP1 |
| OP2 |
(2)t=5时,可求得|
| OP1 |
| OP2 |
解答:解:(1)依题意,e=
=
,
∴e2=
=
=
,a>0,b>0,
∴b=
a,设双曲线C:
-
=1(a>0,b>0)的渐近线l1:y=
x的倾斜角为θ,
则tanθ=
,tan∠P1OP2=tan2θ=
,
∴cos2θ=
,sin2θ=
;
∵
•
=|
|•|
|•cos∠P1OP2=|
|•|
|×
=t,
S△P1OP2=
|
|•|
|•sin∠P1OP2=
|
|•|
|×
=6
∴|
|•|
|=13.
∴t=|
|•|
|×
=13×
=5.
(2)∵t=|
|•|
|×
=5,
∴|
|•|
|=13.
∴由余弦定理得:|P1P2|2=|OP1|2+|OP2|2-2|
|•|
|cos∠P1OP2
≥2|
|•|
|(1-cos∠P1OP2)
=2×13×
=16(当且仅当|
|=|
|时取“=”).
∴|P1P2|≥4(当且仅当|
|=|
|时取“=”).
∵
=λ
(λ>0),
∴P2、P、P1三点共线,又P在双曲线C右支上,
∵S△P1OP2=
|
|•|
|•sin∠P1OP2=
|
|•|
|×
=6,
又S△P1OP2=
|P1P2|•h(h为原点O到直线P1P2的距离),
∴当|
|=|
|=
时,|P1P2|取得最小值4,h取到最大值,此时h=a,即双曲线C的方程中的a取到最大值.
∴
×4a=6,
∴a=3,b=2.
∴双曲线的方程为:
-
=1.
| c |
| a |
| ||
| 3 |
∴e2=
| c2 |
| a2 |
| a2+b2 |
| a2 |
| 13 |
| 9 |
∴b=
| 2 |
| 3 |
| x2 |
| a2 |
| y2 |
| b2 |
| b |
| a |
则tanθ=
| 2 |
| 3 |
| 12 |
| 5 |
∴cos2θ=
| 5 |
| 13 |
| 12 |
| 13 |
∵
| OP1 |
| OP2 |
| OP1 |
| OP2 |
| OP1 |
| OP2 |
| 5 |
| 13 |
S△P1OP2=
| 1 |
| 2 |
| OP1 |
| OP2 |
| 1 |
| 2 |
| OP1 |
| OP2 |
| 12 |
| 13 |
∴|
| OP1 |
| OP2 |
∴t=|
| OP1 |
| OP2 |
| 5 |
| 13 |
| 5 |
| 13 |
(2)∵t=|
| OP1 |
| OP2 |
| 5 |
| 13 |
∴|
| OP1 |
| OP2 |
∴由余弦定理得:|P1P2|2=|OP1|2+|OP2|2-2|
| OP1 |
| OP2 |
≥2|
| OP1 |
| OP2 |
=2×13×
| 8 |
| 13 |
| OP1 |
| OP2 |
∴|P1P2|≥4(当且仅当|
| OP1 |
| OP2 |
∵
| P2P |
| PP1 |
∴P2、P、P1三点共线,又P在双曲线C右支上,
∵S△P1OP2=
| 1 |
| 2 |
| OP1 |
| OP2 |
| 1 |
| 2 |
| OP1 |
| OP2 |
| 12 |
| 13 |
又S△P1OP2=
| 1 |
| 2 |
∴当|
| OP1 |
| OP2 |
| 13 |
∴
| 1 |
| 2 |
∴a=3,b=2.
∴双曲线的方程为:
| x2 |
| 9 |
| y2 |
| 4 |
点评:本题考查直线与圆锥曲线的关系,考查双曲线的简单几何性质,考查二倍角公式、向量的数量积、三角形面积公式、基本不等式的综合应用,考查化归思想与等价转化思想,属于难题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
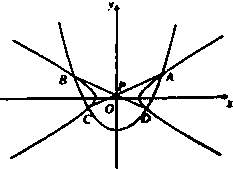 如图,双曲线
如图,双曲线 请考生在(1)(2)中任选一题作答,每小题12分.如都做,按所做的第(1)题计分.
请考生在(1)(2)中任选一题作答,每小题12分.如都做,按所做的第(1)题计分. 请考生在(1)(2)中任选一题作答,每小题12分.如都做,按所做的第(1)题计分.
请考生在(1)(2)中任选一题作答,每小题12分.如都做,按所做的第(1)题计分.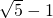 ,求AC的长.
,求AC的长.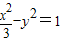 与抛物线x2=3(y+m)相交于A(x1,y1),B(-x1,y1),C(-x2,y2)D(x2,y2),(x1>0,x2>0),直线AC、BD的交点为P(0,p).
与抛物线x2=3(y+m)相交于A(x1,y1),B(-x1,y1),C(-x2,y2)D(x2,y2),(x1>0,x2>0),直线AC、BD的交点为P(0,p).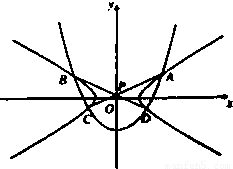
 ,求AC的长.
,求AC的长.