题目内容
9.设全集U=R,A={x|$\frac{x-2}{x+1}$<0},B={y=cosx,x∈A},则A∩B=(cos2,1].分析 求出A中不等式的解集确定出A,求出B中y的范围确定出B,找出A与B的交集即可.
解答 解:由A中不等式变形得:(x-2)(x+1)<0,
解得:-1<x<2,即A=(-1,2),
由B中y=cosx,x∈A,得到cos2<cosx≤1,即B=(cos2,1],
则A∩B=(cos2,1],
故答案为:(cos2,1]
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
2.已知复数z=$\frac{1-2i}{3+4i}$(i是虚数单位),则z的共轭复数的虚部是( )
| A. | -$\frac{2}{5}$i | B. | $\frac{2}{5}$i | C. | -$\frac{2}{5}$ | D. | $\frac{2}{5}$ |
17.如图是一建筑物的三视图(单位:米),现需将其外壁用油漆刷一遍,若每平方米用漆α千克,则共需油漆的总量为( )
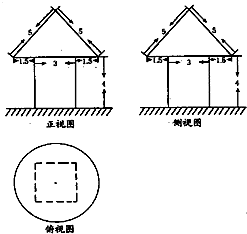

| A. | (48+36π)α千克 | B. | (39+24π)α千克 | C. | (36+36π)α千克 | D. | (36+30π)α千克 |
4.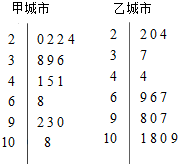 空气质量指数PM2.5 (单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
空气质量指数PM2.5 (单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
甲、乙两城市2015年2月份中的15天对空气质量指数PM2.5进行监测,获得PM2.5日均浓度指数数据如茎叶图所示:
(Ⅰ)根据你所学的统计知识分别写出甲、乙两城市15天内空气质量的中位数,并分析两城市空气质量哪个较好?
(Ⅱ)王先生到乙地出差5天,已知该5天是空气质量最好的五天,王先生要在这5天中选择两天出去游玩,求这两天恰好有一天空气质量类别为优的概率.
 空气质量指数PM2.5 (单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
空气质量指数PM2.5 (单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:| PM2.5日均浓度 | 0~35 | 35~75 | 75~115 | 115~150 | 150~250 | >250 |
| 空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
| 空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
(Ⅰ)根据你所学的统计知识分别写出甲、乙两城市15天内空气质量的中位数,并分析两城市空气质量哪个较好?
(Ⅱ)王先生到乙地出差5天,已知该5天是空气质量最好的五天,王先生要在这5天中选择两天出去游玩,求这两天恰好有一天空气质量类别为优的概率.
18.${({\frac{1+i}{1-i}})^{2015}}$=( )
| A. | i | B. | -1 | C. | 1 | D. | -i |
19.下列函数中,既是偶函数又在区间(0,+∞)上单调递增的是( )
| A. | y=x3 | B. | y=$\sqrt{x}$ | C. | y=cosx | D. | y=2|x| |