题目内容
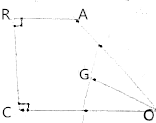
12.如图所示:已知直角梯形ABCO中,∠ABC=∠BCO=90°,AB=1,BC=$\sqrt{3}$,OA=OC=2,设$\overrightarrow{OM}$=m$\overrightarrow{OA}$,$\overrightarrow{ON}$=n$\overrightarrow{OC}$(其中0<m,n<1)G为线段MN的中点.(1)当m=$\frac{1}{2}$时,若O,G,B三点共线,求n的值;
(2)若△OMN的面积为$\frac{\sqrt{3}}{2}$,求|$\overrightarrow{OG}$|的最小值.
分析 (1)以O为坐标原点,OC所在直线为x轴,建立直角坐标系,求得A,B,C,M,N,G的坐标,再由向量共线的坐标表示,计算可得n的值;
(2)求得M,N,G的坐标,由三角形的面积公式,计算可得mn=$\frac{1}{2}$,计算OG的模,由配方,即可得到最小值.
解答  解:(1)以O为坐标原点,OC所在直线为x轴,
解:(1)以O为坐标原点,OC所在直线为x轴,
建立直角坐标系,可得O(0,0),A(1,$\sqrt{3}$),B(2,$\sqrt{3}$),
C(2,0),M($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),N(2n,0),G(n+$\frac{1}{4}$,$\frac{\sqrt{3}}{4}$),
由O,G,B三点共线,可得$\overrightarrow{OG}$∥$\overrightarrow{OB}$,
即有$\frac{\sqrt{3}}{4}$×2=$\sqrt{3}$(n+$\frac{1}{4}$),
解得n=$\frac{1}{4}$;
(2)由$\overrightarrow{OM}$=m$\overrightarrow{OA}$,$\overrightarrow{ON}$=n$\overrightarrow{OC}$,可得M(m,$\sqrt{3}$m),N(2n,0),
可得G(n+$\frac{1}{2}$m,$\frac{\sqrt{3}}{2}$m),
由△OMN的面积为$\frac{\sqrt{3}}{2}$,可得$\frac{1}{2}$×2n×$\sqrt{3}$m=$\frac{\sqrt{3}}{2}$,
即有mn=$\frac{1}{2}$,
则|$\overrightarrow{OG}$|=$\sqrt{(n+\frac{1}{2}m)^{2}+\frac{3}{4}{m}^{2}}$=$\sqrt{{n}^{2}+{m}^{2}+mn}$
=$\sqrt{(m-n)^{2}+3mn}$=$\sqrt{(m-n)^{2}+\frac{3}{2}}$,
当m=n=$\frac{\sqrt{2}}{2}$时,|$\overrightarrow{OG}$|取得最小值,且为$\frac{\sqrt{6}}{2}$.
点评 本题考查向量的坐标运算,考查向量共线的坐标表示,向量的模的最值,考查三角形的面积公式的运用,属于中档题.

 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案| A. | 10 | B. | -10 | C. | 4 | D. | -4 |
| A. | (1,+∞) | B. | (1,8) | C. | (4,8) | D. | [4,8) |
| A. | aa<bb | B. | aa>bb | C. | ab<ba | D. | ab>ba |