题目内容
函数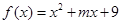 在区间
在区间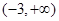 单调递增,则实数
单调递增,则实数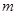 的取值范围为
的取值范围为
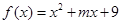 在区间
在区间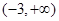 单调递增,则实数
单调递增,则实数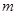 的取值范围为
的取值范围为A.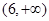 | B.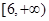 | C.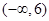 | D.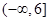 |
B
试题分析:函数
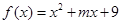 的图象是开口向上的抛物线,以
的图象是开口向上的抛物线,以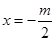 为对称轴,在
为对称轴,在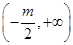 上单调递增,因为在区间
上单调递增,因为在区间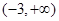 单调递增,所以
单调递增,所以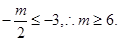
点评:二次函数的单调性是经常考查的内容,二次函数的图象是抛物线,以
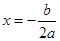 为对称轴,要结合图象数形结合解决问题.
为对称轴,要结合图象数形结合解决问题.
练习册系列答案
相关题目
题目内容
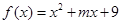 在区间
在区间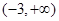 单调递增,则实数
单调递增,则实数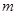 的取值范围为
的取值范围为A.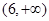 | B.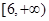 | C.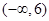 | D.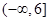 |
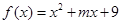 的图象是开口向上的抛物线,以
的图象是开口向上的抛物线,以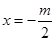 为对称轴,在
为对称轴,在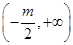 上单调递增,因为在区间
上单调递增,因为在区间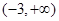 单调递增,所以
单调递增,所以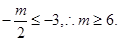
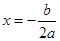 为对称轴,要结合图象数形结合解决问题.
为对称轴,要结合图象数形结合解决问题.