题目内容
某学生在复习指数函数的图象时发现:在y轴左边, y=3x与y=2x的图象均以x轴负半轴为渐近线, 当x=0时, 两图象交于点(0, 1).这说明在y轴的左边y=3x与y=2x的图象从左到右开始时几乎一样, 后来y=2x的图象变化加快使得y=2x与y=3x的图象逐渐远离, 而当x经过某一值x0以后 y= 3x的图象变化加快使得y=2x与y=3x的图象又逐渐接近, 直到x=0时两图象交于点(0, 1).那么x0=( )
A. | B. |
C. | D. |
B
解析试题分析:根据题意,由于指数函数图象变化规律可知,不同底数的指数函数图象,底数大于1时,底数越大的则在y轴右侧越是接近于y轴,在y轴左侧,越来越接近于x轴,那么分界点(0,1),因此可知,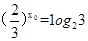 ,
,
考点:指数函数图象
点评:主要是考查了指数函数图象与性质的运用,属于基础题。

练习册系列答案
相关题目
若 ,则函数
,则函数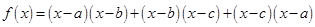 的两个零点分别位于区间 ( )
的两个零点分别位于区间 ( )
A. 和 和 内 内 | B. 和 和 内 内 |
C. 和 和 内 内 | D. 和 和 内 内 |
已知函数 ,则函数
,则函数 的零点个数是( )
的零点个数是( )
| A.4 | B.3 | C.2 | D.1 |
已知函数 若
若 ,则实数
,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
设奇函数 的定义域为R,最小正周期
的定义域为R,最小正周期 ,若
,若 ,则
,则 的取值范围是
的取值范围是
A. | B. |
C. | D. |
设a>1,则log0.2a , 0.2a, a0.2的大小关系是( )
| A.0.2a<log0.2a<a0.2 | B.log0.2a<0.2a<a0.2 |
| C.log0.2a<a0.2<0.2a | D.0.2a<a0.2<log0.2a |
若存在正数x使2x(x-a)<1成立,则a 的取值范围是( )
| A.(-∞,+∞) | B.(-2, +∞) | C.(0, +∞) | D.(-1,+∞) |
已知一元二次不等式 的解集为
的解集为 ,则
,则 的解集为( )
的解集为( )
A. | B. |
C.{x| } } | D.{x|  } } |
 设
设 表示
表示 中的较大值,
中的较大值, 表示
表示 得最小值为
得最小值为
 得最小值为
得最小值为 ,则
,则



