Question

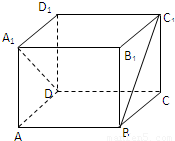
如右图，正方体ABCD-A₁B₁C₁D₁中，
①DA₁与BC₁平行；
②DD₁与BC₁垂直；
③DA₁与BB₁异面；
④A₁B₁与BC₁垂直．
以上四个命题中，正确命题的序号是（ ）

A．③④
B．②③④
C．①②④
D．①④

Answer 1

【答案】分析：根据空间直线的位置关系，结合异面直线的判定方法，可得①不正确且③是真命题；根据异面直线所成角的定义与求法，结合正方体的性质得到DD₁与BC₁所成角是45°，故②不正确；根据正方体的性质和线面垂直的性质，可得④是真命题．由此即可得到本题的答案．
解答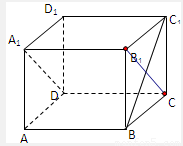：解：对于①，因为A₁B₁∥CD，所以四边形A₁B₁CD是平行四边形
∴B₁C∥DA₁，可得B₁C与BC₁所成的角就等于DA₁与BC₁所成的角
∵正方形BB₁C₁C中，B₁C与BC₁相交且垂直
∴DA₁与BC₁是互相垂直的异面直线，故①不正确；
对于②，因为正方体ABCD-A₁B₁C₁D₁中，DD₁∥BB₁，
而正方形BB₁C₁C中，∠B₁BC₁=45°
∴DD₁与BC₁所成角是45°，并不垂直，故②不正确；
对于③，由于正方体ABCD-A₁B₁C₁D₁中，平面AA₁D₁D∥平面BB₁C₁C
可得DA₁与BB₁分别在两个平行平面中，它们不可能相交
又∵B₁C∥DA₁且B₁C与BB₁相交
∴DA₁与BB₁不平行，必定是异面直线，故③正确；
对于④，因为正方体ABCD-A₁B₁C₁D₁中，直线A₁B₁⊥平面BB₁C₁C
结合直线BC₁?平面BB₁C₁C，可得A₁B₁⊥BC₁，可得④正确
由此可得正确命题的序号为③④
故选：A
点评：本题给出正方体模型，叫我们判定关于异面直线所成角和空间直线位置关系的几个命题的真假．着重考查了正方体的性质、线面垂直的判定与性质和异面直线所成角的定义与求法等知识，属于中档题．