题目内容

20．如图，将边长为1的正方形ABCD，沿对角线BD折起来，使平面ABD⊥平面C′BD，则AC′=（　　）
A．1B．$\frac{1}{2}$C．$\sqrt{2}$D．$\frac{\sqrt{2}}{2}$

分析 将边长为1的正方形ABCD沿对角线BD折起来，使平面ABD⊥平面C′BD，通过解三角形求出AC′．

解答 解：取BD的中点O，连接OA，OC′，则
∵将边长为1的正方形ABCD沿对角线BD折起来，使平面ABD⊥平面C′BD，
∴AO⊥CO，AO=CO=$\frac{\sqrt{2}}{2}$，
∴AC′=$\sqrt{（\frac{\sqrt{2}}{2}）^{2}+（\frac{\sqrt{2}}{2}）^{2}}$=1
故选：A．

点评 本题是基础题，考查平面图形的折叠与展开，求出两点之间的距离，正确处理折叠前后的关系是解好这类问题的关键．

练习册系列答案
相关题目
10．已知（1-2x）7=a0+a1x+a2x2+…a7x7，
（1）求（a0+a2+a4+a6）2-（a1+a3+a5+a7）2的值；
（2）求|ai|（其中i=1，2，…，7）的最大值．
11．已知a，b∈R，函数f（x）=a+ln（x+1）的函数与g（x）=$\frac{1}{3}$x3-$\frac{1}{2}$x2+bx的图象交点（0，0）处有公共切线．
（1）证明：不等式f（x）≤g（x）对一切x∈（-1，+∞）恒成立；
（2）设-1＜x1＜x2，当x∈（x1，x2）时，证明：$\frac{f（x）-f（{x}_{1}）}{x-{x}_{1}}$＞$\frac{f（x）-f（{x}_{2}）}{x-{x}_{2}}$．
8．如图，四边形ABCD为矩形，AD⊥平面ABE，F为CE上中点，且BF⊥平面ACE．
（1）求证：AE∥平面BFD；
（2）求证：AE⊥平面BCE．
15．已知函数f（x）为R上的奇函数，且当x≥0时，f（x）=3x-a，则f（-2）=（　　）
A．-10B．-8C．10D．8
5．过椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$（a＞b＞0）的焦点F作弦AB，若丨AF丨=d1，丨FB丨=d2，那么$\frac{1}{{d}_{1}}+\frac{1}{{d}_{2}}$的值为$\frac{2a}{{b}^{2}}$．
12．已知曲线y=x2+2x-1在点M处的切线与x轴平行，则点M的坐标是（　　）
A．（-2，2）B．（-2，-2）C．（-1，2）D．（-1，-2）
9．如图，PA⊥面ABC，△ABC中BC⊥AC，则△PBC是（　　）
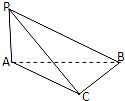
A．直角三角形B．锐角三角形C．钝角三角形D．以上都有可能
10．若函数f（x）=$\frac{sinx}{x}$，并且$\frac{π}{3}$＜a＜b＜$\frac{2π}{3}$，则下列各结论中正确的是（　　）
A．f（a）＜f（$\sqrt{ab}$）＜f（$\frac{a+b}{2}$）B．f（$\sqrt{ab}$）＜f（$\frac{a+b}{2}$）＜f（b）C．f（$\sqrt{ab}$）＜f（$\frac{a+b}{2}$）＜f（a）D．f（b）＜f（$\frac{a+b}{2}$）＜f（$\sqrt{ab}$）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网