题目内容
(本小题满分12分)为了了解某工厂开展群众体育活动的情况,拟采用分层抽样的方法从A,B,C三个区中抽取7个工厂进行调查,已知A,B,C区中分别有18,27,18个工厂
(Ⅰ)求从A,B,C区中分别抽取的工厂个数;
(Ⅱ)若从抽取的7个工厂中随机抽取2个进行调查结果的对比,求这2个工厂中至少有1个来自A区的概率。
(Ⅰ)求从A,B,C区中分别抽取的工厂个数;
(Ⅱ)若从抽取的7个工厂中随机抽取2个进行调查结果的对比,求这2个工厂中至少有1个来自A区的概率。
(1)2,3,2. (2)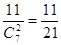
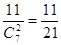
(1)工厂总数为18+27+18=63,样本容量与总体中的个体数比为 ,所以从A,B,C三个区中应分别抽取的工厂个数为2,3,2.
,所以从A,B,C三个区中应分别抽取的工厂个数为2,3,2.
(2)设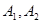 为在A区中抽得的2个工厂,
为在A区中抽得的2个工厂,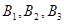 为在B区中抽得的3个工厂,
为在B区中抽得的3个工厂,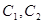 为在C区中抽得的2个工厂,这7个工厂中随机的抽取2个,全部的可能结果有:
为在C区中抽得的2个工厂,这7个工厂中随机的抽取2个,全部的可能结果有: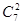 种,随机的抽取的2个工厂至少有一个来自A区的结果有
种,随机的抽取的2个工厂至少有一个来自A区的结果有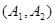 ,
,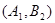



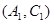 ,同理
,同理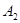 还能组合5种,一共有11种.
还能组合5种,一共有11种.
所以所求的概率为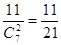
思路分析:(1)先求出工厂总数为18+27+18=63,根据分层抽样的特点得A,B,C三个区中应分别抽取的工厂个数为2,3,2;(2)根据排列组合的原理得从7个工厂中随机的抽取2个,全部的可能结果有: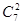 种,满足条件的共有11种,由古典概型的概率公式得所求的概率为
种,满足条件的共有11种,由古典概型的概率公式得所求的概率为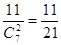 。
。
 ,所以从A,B,C三个区中应分别抽取的工厂个数为2,3,2.
,所以从A,B,C三个区中应分别抽取的工厂个数为2,3,2.(2)设
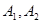 为在A区中抽得的2个工厂,
为在A区中抽得的2个工厂,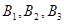 为在B区中抽得的3个工厂,
为在B区中抽得的3个工厂,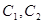 为在C区中抽得的2个工厂,这7个工厂中随机的抽取2个,全部的可能结果有:
为在C区中抽得的2个工厂,这7个工厂中随机的抽取2个,全部的可能结果有: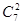 种,随机的抽取的2个工厂至少有一个来自A区的结果有
种,随机的抽取的2个工厂至少有一个来自A区的结果有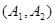 ,
,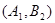



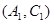 ,同理
,同理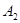 还能组合5种,一共有11种.
还能组合5种,一共有11种.所以所求的概率为
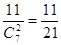
思路分析:(1)先求出工厂总数为18+27+18=63,根据分层抽样的特点得A,B,C三个区中应分别抽取的工厂个数为2,3,2;(2)根据排列组合的原理得从7个工厂中随机的抽取2个,全部的可能结果有:
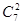 种,满足条件的共有11种,由古典概型的概率公式得所求的概率为
种,满足条件的共有11种,由古典概型的概率公式得所求的概率为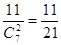 。
。
练习册系列答案
相关题目
 人,青年人
人,青年人 人,为调查身体健康状况,需要从中抽取一个容量为
人,为调查身体健康状况,需要从中抽取一个容量为 的样本,用分层抽样方法应分别从老年人、中年人、青年人中应各抽取
的样本,用分层抽样方法应分别从老年人、中年人、青年人中应各抽取  )无法看清,若统计员计算无误,则数字
)无法看清,若统计员计算无误,则数字




 依次为
依次为 .现从一批该日用品中抽取200件,对其等级系数进行统计分析,得到频率
.现从一批该日用品中抽取200件,对其等级系数进行统计分析,得到频率 的分布表如下:
的分布表如下:
 的件数为 ________.
的件数为 ________. 的样本,已知从女生中抽取的人数为80,则
的样本,已知从女生中抽取的人数为80,则 的方差为2,则数据
的方差为2,则数据 的方差为 .
的方差为 .