题目内容

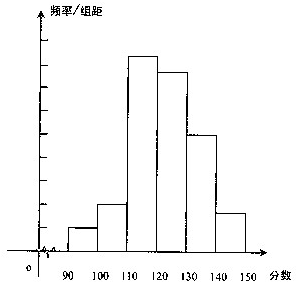某学校2012届高三高考前最后一次摸拟考试数学成绩统计整理后，画出频率分布直方图（如图），图中从左到右各小方形面积之比为（2：4：17：15：9：3，）其中成绩为100～110人数为28，则成绩为140～150的人数为
21
21
．
分析：先求得这两段的人数所占的比例，再根据这两段的人数所占的比例之比等于这两段的人数之比，求得成绩为140～150的人数．
解答：解：由题意可得成绩为100～110人数为28所占的比例为
4
2+4+17+15+9+3
=
4
50
，
成绩为140～150的人数所占的比列为
3
2+4+17+15+9+3
=
3
50
，
设成绩为140～150的人数为x，则由
4
50
3
50
=
28
x
，解得 x=21，
故答案为 21．
点评：本题主要考查频率分步直方图的应用，属于基础题．
练习册系列答案
相关题目
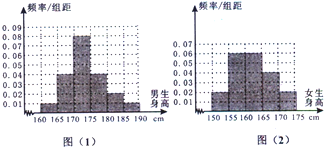2、某学校为了调查高三年级的200名文科学生完成课后作业所需时间，采取了两种抽样调查的方式：第一种由学生会的同学随机抽取20名同学进行调查；第二种由教务处对该年级的文科学生进行编号，从001到200，抽取学号最后一位为2的同学进行调查，则这两种抽样的方法依次为（　　）
（2012•泉州模拟）某学校为调查高三年学生的身高情况，按随机抽样的方法抽取80名学生，得到男生身高情况的频率分布直方图（图（1）和女生身高情况的频率分布直方图（图（2））．已知图（1）中身高在170～175cm的男生人数有16人．
（I）试问在抽取的学生中，男、女生各有多少人？
（II）根据频率分布直方图，完成下列的2×2列联表，并判断能有多大（百分几）的把握认为“身高与性别有关”？
≥170cm ＜170cm 总计
男生身高
女生身高
总计
（Ⅲ）在上述80名学生中，从身高在170～175cm之间的学生按男、女性别分层抽样的方法，抽出5人，从这5人中选派3人当旗手，求3人中恰好有一名女生的概率．
（2010•桂林二模）（注意：在试题卷上作答无效）
桂林某学校从参加高三年级第二次模拟考试的学生中随机抽出100名学生，将其数学成绩（均为整数）分成五段[50，70），[70，90），[90，110），[110，130），[130，150]后得到如右部分频率分布直方图，分析图形的信息，回答下列问题：
（Ⅰ）求分数在[90，110）内的频率和学生数，并补全这个频率分布直方图；
（Ⅱ）现从分数段[90，150]的学生中随机抽取2人给予助学金奖励，抽到的学生成绩在[90，110）内每人奖励100元，在[100，130）内每人奖励200元，在[130，150）内每人奖励300元，用ξ表示抽取结束后总的奖励金额，求ξ的分布列和数学期望．
某学校为调查高三年学生的身高情况，按随机抽样的方法抽取80名学生，得到男生身高情况的频率分布直方图（图（1））和女生身高情况的频率分布直方图（图（2））．已知图（1）中身高在170～175cm的男生人数有16人．

（Ⅰ）试问在抽取的学生中，男、女生各有多少人？
（Ⅱ）根据频率分布直方图，完成下列的2×2列联表，并判断能有多大（百分儿）的把握认为“身高与性别有关”？
附：
P（x2≥k） 0.05 0.01
k 3.841 6.635
  ≥170cm ＜170cm 总计
男生身高      
女生身高      
总计      
x2=
n(n11n22-n12n21)2
n1+n2+n1+n2

（Ⅲ）在上述80名学生中，从身高在170～175cm之间的学生中按男、女性别分层抽样的方法，抽出5人，从这5人中选派3人当旗手，求3人中恰好有一名女生的概率．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网