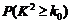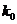题目内容

(Ⅰ)试问在抽取的学生中,男、女生各有多少人?
(Ⅱ)根据频率分布直方图,完成下列的2×2列联表,并判断能有多大(百分儿)的把握认为“身高与性别有关”?
附:
| P(x2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
| ≥170cm | <170cm | 总计 | |
| 男生身高 | |||
| 女生身高 | |||
| 总计 |
| n(n11n22-n12n21)2 |
| n1+n2+n1+n2 |
(Ⅲ)在上述80名学生中,从身高在170~175cm之间的学生中按男、女性别分层抽样的方法,抽出5人,从这5人中选派3人当旗手,求3人中恰好有一名女生的概率.
(Ⅱ)男生身高≥170cm的人数=(0.08+0.04+0.02+0.01)×5×40=30,女生身高≥170cm的人数为0.02×5×40=4,从而可得列联表,利用公式,求得K2,与临界值比较后,即可得到结论;
(Ⅲ)在170~175cm之间的男生有16人,女生人数有4人,按分层抽样的方法抽出5人,则男生占4人,女生占1人. 利用列举法确定从5人任选3名的所有可能,3人中恰好有一名女生的所有可能,即可求得概率.
设男生数为n1,则0.4=
| 16 |
| n1 |
由男生的人数为40,得女生的人数为80-40=40.
(Ⅱ)男生身高≥170cm的人数=(0.08+0.04+0.02+0.01)×5×40=30,
女生身高≥170cm的人数为0.02×5×40=4,
所以可得到下列列联表:
| ≥170cm | <170cm | 总计 | |
| 男生身高 | 30 | 10 | 40 |
| 女生身高 | 4 | 36 | 40 |
| 总计 | 34 | 46 | 80 |
| 80(30×36-10×4)2 |
| 40×40×34×46 |
(Ⅲ)在170~175cm之间的男生有16人,女生人数有4人,按分层抽样的方法抽出5人,则男生占4人,女生占1人.
设男生为A1,A2,A3,A4,女生为B.
从5人任选3名有:(A1,A2,A3),(A1,A2,A4),(A1,A2,B),(A1,A3,A4),(A1,A3,B),(A1,A4,B),(A2,A3,A4),(A2,A3,B),(A2,A4,B),(A3,A4,B),共10种可能,
3人中恰好有一名女生有:(A1,A2,B),(A1,A3,B),(A1,A4,B),(A2,A3,B),(A2,A4,B),(A3,A4,B),共6种可能,
故所求概率为
| 6 |
| 10 |
| 3 |
| 5 |

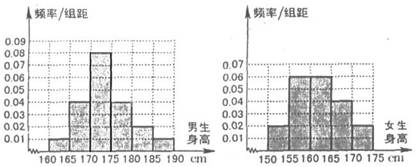
某学校为调查高三年学生的身高情况,按随机抽样的方法抽取80名学生,得到男生身高情况的频率分布直方图(图(1))和女生身高情况的频率分布直方图(图(2)).已知图(1)中身高在170 ~175cm的男生人数有16人.
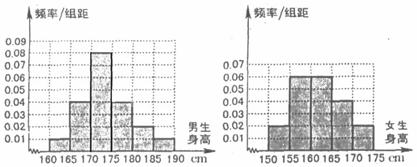
图(1) 图(2)
(Ⅰ)试问在抽取的学生中,男、女生各有多少人?
(Ⅱ)根据频率分布直方图,完成下列的2×2列联表,并判断能有多大(百分几)的把握认为“身高与性别有关”?
| ≥170cm | <170cm | 总计 | |
| 男生身高 | |||
| 女生身高 | |||
| 总计 |
(Ⅲ)在上述80名学生中,从身高在170~175cm之间的学生中按男、女性别分层抽样的方法,抽出5人,从这5人中选派3人当旗手,求3人中恰好有一名女生的概率.
参考公式: ![]()
参考数据:
|
| 0.025 | 0.010 | 0.005 | 0.001 |
|
| 5.024 | 6.635 | 7.879 | 10.828 |
(I)试问在抽取的学生中,男、女生各有多少人?
(II)根据频率分布直方图,完成下列的2×2列联表,并判断能有多大(百分几)的把握认为“身高与性别有关”?
| ≥170cm | <170cm | 总计 | |
| 男生身高 | |||
| 女生身高 | |||
| 总计 |
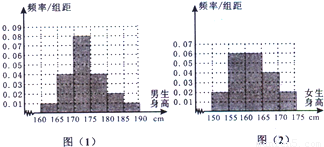
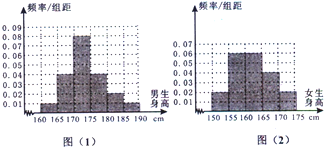
某学校为调查高三年学生的身高情况,按随机抽样的方法抽取80名学生,得到男生身高情况的频率分布直方图(图(1))和女生身高情况的频率分布直方图(图(2)).已知图(1)中身高在170 ~175cm的男生人数有16人.
图(1) 图(2)
(Ⅰ)试问在抽取的学生中,男、女生各有多少人?
(Ⅱ)根据频率分布直方图,完成下列的2×2列联表,并判断能有多大(百分几)的把握认为“身高与性别有关”?
|
|
≥170cm |
<170cm |
总计 |
|
男生身高 |
|
|
|
|
女生身高 |
|
|
|
|
总计 |
|
|
|
(Ⅲ)在上述80名学生中,从身高在170~175cm之间的学生中按男、女性别分层抽样的方法,抽出5人,从这5人中选派3人当旗手,求3人中恰好有一名女生的概率.
参考公式: 
参考数据:
|
|
0.025 |
0.010 |
0.005 |
0.001 |
|
|
5.024 |
6.635 |
7.879 |
10.828 |
 (2012•泉州模拟)某学校为调查高三年学生的身高情况,按随机抽样的方法抽取80名学生,得到男生身高情况的频率分布直方图(图(1)和女生身高情况的频率分布直方图(图(2)).已知图(1)中身高在170~175cm的男生人数有16人.
(2012•泉州模拟)某学校为调查高三年学生的身高情况,按随机抽样的方法抽取80名学生,得到男生身高情况的频率分布直方图(图(1)和女生身高情况的频率分布直方图(图(2)).已知图(1)中身高在170~175cm的男生人数有16人.