题目内容
给出四个命题:
(1)函数在闭区间[a,b]上的极大值一定比极小值大
(2)函数在闭区间[a,b]上的最大值一定是极大值
(3)对于f(x)=x3+px2+2x+1,若|p|<
,则f(x)无极值
(4)函数f(x)在区间(a,b)上一定不存在最值
其中正确命题的个数是( )
(1)函数在闭区间[a,b]上的极大值一定比极小值大
(2)函数在闭区间[a,b]上的最大值一定是极大值
(3)对于f(x)=x3+px2+2x+1,若|p|<
| 6 |
(4)函数f(x)在区间(a,b)上一定不存在最值
其中正确命题的个数是( )
分析:应用极值与最值的概念逐一判断即可,函数的极大值指的是比它附近其他点的函数值都大的函数值,极小值指的是比它附近其他点的函数值都小的函数值,但是极大值不一定比极小值大,可判断(1)的对错,函数在闭区间上的最值在端点或极值处取得,可判断(2),(4)的对错,利用导数的取值范围可判断函数的极值存在情况,可判断(3)的对错.
解答:解:(1)函数在闭区间[a,b]上的极大值指的是比它附近其他点的函数值都大的函数值,
极小值指的是比它附近其他点的函数值都小的函数值,但极大值不一定大于极小值,∴(1)错误.
(2)函数在闭区间[a,b]上的最大值可能是极大值,也可能是端点函数值,∴(2)错误.
(3)对函数f(x)=x3+px2+2x+1求导,得,f′(x)=3x2+2px+2,
当|p|<
时,△=4p2-24<0,函数f(x)=x3+px2+2x+1在R上为减函数,无极值,∴(3)正确.
(4)若函数f(x)在区间(a,b)上先增后减,则函数f(x)在区间(a,b)上有最大值,
若函数f(x)在区间(a,b)上先减后增,则函数f(x)在区间(a,b)上有最小值,∴(4)错误
故选B
极小值指的是比它附近其他点的函数值都小的函数值,但极大值不一定大于极小值,∴(1)错误.
(2)函数在闭区间[a,b]上的最大值可能是极大值,也可能是端点函数值,∴(2)错误.
(3)对函数f(x)=x3+px2+2x+1求导,得,f′(x)=3x2+2px+2,
当|p|<
| 6 |
(4)若函数f(x)在区间(a,b)上先增后减,则函数f(x)在区间(a,b)上有最大值,
若函数f(x)在区间(a,b)上先减后增,则函数f(x)在区间(a,b)上有最小值,∴(4)错误
故选B
点评:本题主要考查函数的极值与最值的概念,因为是多选题,需要逐一判断.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
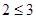 ; (2)如果
; (2)如果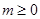 , 则方程
, 则方程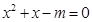 有实根; (3)
有实根; (3)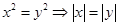 ; (4)“
; (4)“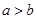 ”是 “
”是 “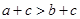 ”的充要条件,其中正确命题的个数有( )个
”的充要条件,其中正确命题的个数有( )个