题目内容
给出四个命题:
(1)2≤3;
(2)如果m≥0,则方程x2+x-m=0有实根;
(3)x2=y2⇒|x|=|y|;
(4)“a>b”是“a+c>b+c”的充要条件,
其中正确命题的个数有( )个.
(1)2≤3;
(2)如果m≥0,则方程x2+x-m=0有实根;
(3)x2=y2⇒|x|=|y|;
(4)“a>b”是“a+c>b+c”的充要条件,
其中正确命题的个数有( )个.
分析:通过或命题判断(1)的正误;利用判别式判断(2)的正误;利用方程的等价转换判断(3)的正误;通过不等式的基本性质判断(4)的正误.
解答:解:对于(1):2≤3;满足或命题,所以正确;
对于(2):如果m≥0,则方程x2+x-m=0有实根;因为△=1+4m>0,所以方程有实数根,正确.
对于(3):x2=y2⇒|x|=|y|,满足方程的等价转换,同解变形,所以正确;
对于(4):“a>b”是“a+c>b+c”的充要条件,满足不等式的基本性质,所以正确;
正确命题的个数有4个.
故选D.
对于(2):如果m≥0,则方程x2+x-m=0有实根;因为△=1+4m>0,所以方程有实数根,正确.
对于(3):x2=y2⇒|x|=|y|,满足方程的等价转换,同解变形,所以正确;
对于(4):“a>b”是“a+c>b+c”的充要条件,满足不等式的基本性质,所以正确;
正确命题的个数有4个.
故选D.
点评:本题考查命题的真假的判断,基本知识的应用,基础题,常考题型.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
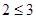 ; (2)如果
; (2)如果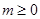 , 则方程
, 则方程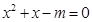 有实根; (3)
有实根; (3)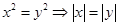 ; (4)“
; (4)“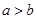 ”是 “
”是 “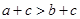 ”的充要条件,其中正确命题的个数有( )个
”的充要条件,其中正确命题的个数有( )个