题目内容
(2011•门头沟区一模)在△ABC中,a、b、c分别为内角A、B、C的对边,且a2=b2+c2+bc.
(1)求角A的大小;
(2)若sinB+sinC=1,试判断△ABC的形状.
(1)求角A的大小;
(2)若sinB+sinC=1,试判断△ABC的形状.
分析:(1)利用余弦定理表示出cosA,把已知的等式变形后代入,求出cosA的值,由A为三角形的内角,利用特殊角的三角函数值即可求出A的度数;
(2)利用正弦定理化简已知的等式,把A的度数代入,利用特殊角的三角函数值及完全平方公式化简后,将sinB+sinC=1代入求出sinBsinC的值,与sinB+sinC=1联立,求出sinB和sinC的值,得到sinB=sinC,由A为钝角,得到B和C都为锐角,可得B=C,可得三角形为顶角是钝角的等腰三角形.
(2)利用正弦定理化简已知的等式,把A的度数代入,利用特殊角的三角函数值及完全平方公式化简后,将sinB+sinC=1代入求出sinBsinC的值,与sinB+sinC=1联立,求出sinB和sinC的值,得到sinB=sinC,由A为钝角,得到B和C都为锐角,可得B=C,可得三角形为顶角是钝角的等腰三角形.
解答:解:(1)∵a2=b2+c2+bc,即b2+c2-a2=-bc,
∴由余弦定理得:cosA=
=-
,…(2分)
又A为三角形的内角,
则A=120°;…(6分)
(2)由正弦定理化简已知的等式得:
sin2A=sin2B+sin2C+sinBsinC,…(7分)
把A=120°代入,化简得:
=(sinB+sinC)2-sinBsinC,
又sinB+sinC=1①,可得sinBsinC=
②,
联立①②,解得:sinB=sinC=
,…(10分)
由(1)知A=120°,可得0<B<90°,0<C<90°,
∴B=C,
则△ABC是顶角是钝角的等腰三角形. …(12分)
∴由余弦定理得:cosA=
| b2+c2-a2 |
| 2bc |
| 1 |
| 2 |
又A为三角形的内角,
则A=120°;…(6分)
(2)由正弦定理化简已知的等式得:
sin2A=sin2B+sin2C+sinBsinC,…(7分)
把A=120°代入,化简得:
| 3 |
| 4 |
又sinB+sinC=1①,可得sinBsinC=
| 1 |
| 4 |
联立①②,解得:sinB=sinC=
| 1 |
| 2 |
由(1)知A=120°,可得0<B<90°,0<C<90°,
∴B=C,
则△ABC是顶角是钝角的等腰三角形. …(12分)
点评:此题考查了解三角形,以及三角形形状的判断,涉及的知识有:正弦、余弦定理,完全平方公式的应用,等腰三角形的判定,以及特殊角的三角函数值,正弦、余弦定理很好的建立了三角形的边角关系,熟练掌握定理是解本题的关键.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
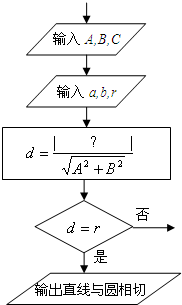 (2011•门头沟区一模)如图所示为一个判断直线Ax+By+C=0与圆(x-a)2+(y-b)2=r2的位置关系的程序框图的一部分,在?处应该填上
(2011•门头沟区一模)如图所示为一个判断直线Ax+By+C=0与圆(x-a)2+(y-b)2=r2的位置关系的程序框图的一部分,在?处应该填上