题目内容
（2011•门头沟区一模）已知定义在R上的函数f（x）是周期函数，且满足f（x-a）=-f（x）（a＞0），函数f（x）的最小正周期为
2a
2a
．分析：先根据条件f（x-a）=-f（x）（a＞0）恒成立可得f（x-2a）=-f（x-a）=f（x）（a＞0），再根据函数周期性的定义可求得函数的最小正周期．
解答：解：∵f（x-a）=-f（x）（a＞0），
∴f（x-2a）=-f（x-a）=f（x）（a＞0）即f（x-2a）=f（x），
根据函数周期性的定义可知函数的最小正周期为2a
故答案为：2a
∴f（x-2a）=-f（x-a）=f（x）（a＞0）即f（x-2a）=f（x），
根据函数周期性的定义可知函数的最小正周期为2a
故答案为：2a
点评：本题主要考查了抽象函数的周期性，以及最小正周期的概念，属于基础题之列．
练习册系列答案
相关题目
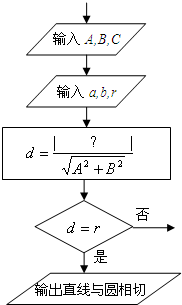（2011•门头沟区一模）如图所示为一个判断直线Ax+By+C=0与圆（x-a）2+（y-b）2=r2的位置关系的程序框图的一部分，在？处应该填上