Question

【题目】(导学号：05856332)

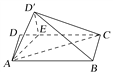
已知三棱柱ABC－A1B1C1如图所示，其中CA⊥平面ABB1A1，四边形ABB1A1为菱形，∠AA1B1＝60°，E为BB1的中点，F为CB1的中点．

(Ⅰ)证明：平面AEF⊥平面CAA1C1；

(Ⅱ)若CA＝2，AA1＝4，求B1到平面AEF的距离．

Answer 1

【答案】(1)见解析(2)

【解析】试题分析：（1）由四边形ABB1A1为菱形，∠AA1B1=60°=∠ABB1，利用等边三角形的性质可得AE⊥BB1，AE⊥AA1．利用线面垂直的性质可得：AE⊥AC，于是AE⊥平面CAA1C1，平面AEF⊥平面CAA1C1．

（2）利用等积法建立所求量的方程，解之即可.

试题解析：

(Ⅰ)∵四边形ABB1A1是菱形，∠AA1B1＝60°＝∠ABB1，

∴△ABB1是正三角形，又BE＝B1E，∴AE⊥BB1，又AA1∥BB1，则AE⊥AA1，

∵CA⊥平面ABB1A1，AE平面ABB1A1，∴CA⊥AE；

又AA1∩CA＝A，∴AE⊥平面CAA1C1，

而AE平面AEF，

∴平面AEF⊥平面CAA1C1.

(Ⅱ)因为E为BB1的中点，F为CB1的中点，所以三角形AEB1的面积S△AEB1＝S△ABB1＝××4×4sin 60°＝2，点F到平面AEB1的距离h＝AC＝1，所以三棱锥A－EFB1的体积VA－EFB1＝VF－EAB1＝×2×1＝.又AE＝4×＝2，AF＝B1C＝，EF＝BC＝，

∴△AEF的面积S△AEF＝×2×＝，设B1到平面AEF的距离为h1，则×h1＝，∴h1＝.∴B1到平面AEF的距离为.