题目内容
如图所示,已知正三棱锥A―BCD中,E、F分别是棱AB、BC的中点,EF⊥DE,且BC=2.
(1)求此正三棱锥的高;
(2)求二面角E―FD―B的大小.

解:解法一:(1)由正三棱锥的性质知AC⊥BD.
∵EF//AC,∴EF⊥BD.又FF⊥ED.故EF⊥平面ABD,
即AC⊥平面ABD,∴AC⊥AB,AC⊥AD.
又∵A―BCD为正三棱锥,∴AB⊥AD,
从而AB=AC=AD=![]() BC=
BC=![]()
设ABCD中心为O,则棱锥高为
AO=![]()
=![]()

(2)过E作EF⊥BO于H,则EH//AO,即
EH⊥平面BCD。又过H作HG⊥DF于G,
连接EG,则EG⊥DF,故∠HGE为二面角E FD―B的平面角,如图a所示.
∵EH=![]() AO=
AO=![]() ,HG=
,HG=![]() BF=
BF=![]() ,
,
∴![]() ,
,
∠EGH=![]() .
.
解法二:
(1)建立如图b所示的空间直角坐标系,
则B、C、D坐标为B(0,0,0)、C(![]() ,1,0)、D(0,2,0),
,1,0)、D(0,2,0),
若设棱锥高为h,又A在BCD面上的射影为△BCD中心,
则A的坐标为(![]() ,1,h).
,1,h).

∵E、F 为AB、BC的中点,∴E(![]() ,
,![]() ,
,![]() ),
),
F(![]() ,
,![]() ,0)
,0)
∵EF⊥DE,∴![]()
即(![]() ,0,
,0,![]() )?(
)?(![]() ,
,![]() ,
,![]() )=0
)=0
∴![]() ,
,![]()
(2)设![]() 为平面DEF的法向量,则
为平面DEF的法向量,则

即
令z=1,则m=(![]() ,
,![]() ,1).
,1).
又平面BCD的法向量为n=(0,0,1),由m、n的方向知,
当二面角E―FD―B设为![]() 时,cos
时,cos![]() =
=![]() ,
,![]()

练习册系列答案
相关题目
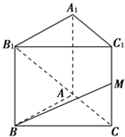 如图所示,已知正三棱柱ABC-A1B1C1的各条棱长都相等,M是侧棱CC1的中点,则异面直线AB1和BM所成的角的大小是
如图所示,已知正三棱柱ABC-A1B1C1的各条棱长都相等,M是侧棱CC1的中点,则异面直线AB1和BM所成的角的大小是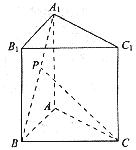
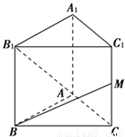 如图所示,已知正三棱柱ABC-A1B1C1的各条棱长都相等,M是侧棱CC1的中点,则异面直线AB1和BM所成的角的大小是 .
如图所示,已知正三棱柱ABC-A1B1C1的各条棱长都相等,M是侧棱CC1的中点,则异面直线AB1和BM所成的角的大小是 . 如图所示,已知正三棱柱ABC-A1B1C1的各条棱长都相等,M是侧棱CC1的中点,则异面直线AB1和BM所成的角的大小是 .
如图所示,已知正三棱柱ABC-A1B1C1的各条棱长都相等,M是侧棱CC1的中点,则异面直线AB1和BM所成的角的大小是 .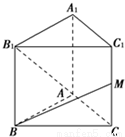 如图所示,已知正三棱柱ABC-A1B1C1的各条棱长都相等,M是侧棱CC1的中点,则异面直线AB1和BM所成的角的大小是 .
如图所示,已知正三棱柱ABC-A1B1C1的各条棱长都相等,M是侧棱CC1的中点,则异面直线AB1和BM所成的角的大小是 .