题目内容
【题目】吉安一中举行了一次“环保知识竞赛”活动,为了解本了次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为![]() 分)作为样本(样本容量为
分)作为样本(样本容量为![]() )进行统计.按照
)进行统计.按照 ![]() 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在![]() 的数据).
的数据).
(1)求样本容量![]() 和频率分布直方图中的
和频率分布直方图中的![]() 的值;
的值;
(2)在选取的样本中,从竞赛学生成绩是![]() 分以上(含
分以上(含![]() 分)的同学中随机抽取
分)的同学中随机抽取![]() 名同学到市政广场参加环保知识宣传的志愿者活动,求所抽取的
名同学到市政广场参加环保知识宣传的志愿者活动,求所抽取的![]() 名同学中得分在
名同学中得分在![]() 的学生人数恰有一人的概率.
的学生人数恰有一人的概率.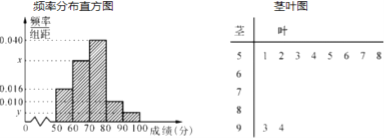
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)根据频率![]() 频数
频数![]() 样本容量, 可得
样本容量, 可得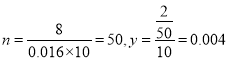 ,再根据频率之和为
,再根据频率之和为![]() ,可求
,可求![]() 的值;(2)则由树形图知:基本时间的总数为
的值;(2)则由树形图知:基本时间的总数为![]() ,事件
,事件![]() 包含基本事件的个数为
包含基本事件的个数为![]() ,所以
,所以![]() .
.
试题解析:(1)由题意可知,样本容量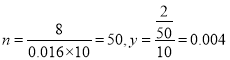 ,又由
,又由![]() ,得
,得![]() .
.
(2)由题意可知,分数在![]() 有
有![]() 人,分别记为:
人,分别记为:![]() ,分数在
,分数在![]() 有
有![]() 人,分别记为:
人,分别记为:![]() ,共
,共![]() 人,记“所抽取的
人,记“所抽取的![]() 名同学中得分在
名同学中得分在![]() 的学生个数恰有一人” 为事件
的学生个数恰有一人” 为事件![]() ,则由树形图知:基本时间的总数为
,则由树形图知:基本时间的总数为![]() ,事件
,事件![]() 包含基本事件的个数为
包含基本事件的个数为![]() ,所以
,所以![]() .
.


练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
【题目】某商店为了吸引顾客,设计了一个摸球小游戏,顾客从装有1个红球,1个白球,3个黑球的袋中一次随机的摸2个球,设计奖励方式如下表:
结果 | 奖励 |
1红1白 | 10元 |
1红1黑 | 5元 |
2黑 | 2元 |
1白1黑 | 不获奖 |
(1)某顾客在一次摸球中获得奖励X元,求X的概率分布表与数学期望;
(2)某顾客参与两次摸球,求他能中奖的概率.