题目内容
(本小题满分12分)
已知函数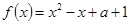
⑴ 若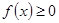 对一切实数x恒成立,求实数a的取值范围。
对一切实数x恒成立,求实数a的取值范围。
⑵ 求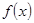 在区间
在区间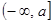 上的最小值
上的最小值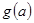 的表达式。
的表达式。
【答案】
⑴ 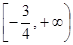 ;⑵
;⑵ 
【解析】本试题主要是考查了二次函数的性质和不等式的综合运用。
(1)因为由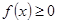 对
对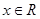 恒成立,即
恒成立,即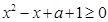 恒成立
恒成立
∴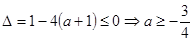
(2)∵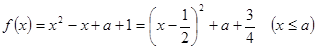
结合对称轴和定义域分类讨论得到最值。
解:⑴ 由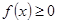 对
对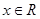 恒成立,即
恒成立,即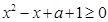 恒成立
恒成立
∴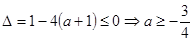 ∴实数a的取值范围为
∴实数a的取值范围为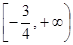
⑵ ∵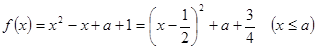
1°:当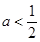 时,
时,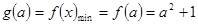
2°:当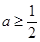 时,
时,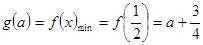
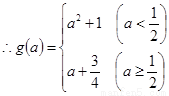

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目