题目内容
【题目】如图,在棱长都相等的正三棱柱![]() 中,
中,![]() 分别为
分别为![]() 的中点.
的中点.

(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() 平面
平面![]() .
.
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)取![]() 中点
中点![]() ,连结
,连结![]() ,根据三角形中位线定理及棱柱的性质可证明四边形
,根据三角形中位线定理及棱柱的性质可证明四边形![]() 是平行四边形,得出
是平行四边形,得出![]() ,由线面平行的判定定理可得
,由线面平行的判定定理可得![]() 平面
平面![]() ;(2)先证明
;(2)先证明![]() 平面
平面![]() ,得出
,得出![]() ,故而
,故而![]() 结合
结合![]() ,根据线面垂直的判定定理可得出
,根据线面垂直的判定定理可得出![]() 平面
平面![]() .
.
试题解析:(1)∵G,E分别为CB,CB1的中点,∴EG∥BB1,且![]() ,
,
又∵正三棱柱ABC﹣A1B1C1,∴EG∥AD,EG=AD
∴四边形ADEG为平行四边形.∴AG∥DE
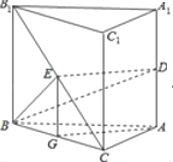
∵AG平面ABC,DE平面ABC,所以 DE∥平面AB
(2)由可得,取BC中点G,∵正三棱柱ABC﹣A1B1C1,
∴BB1⊥平面ABC.∵AG平面ABC, ∴AG⊥BB1,
∵G为BC的中点,AB=AC,
∴AG⊥BC∴AG⊥平面BB1C1C,
∵B1C平面BB1C1C,∴AG⊥B1C,
∵AG∥DE,∴DE⊥B1C,
∵BC=BB1,B1E=EC,∴B1C⊥BE,
∵BE平面BDE,
DE平面BDEBE∩DE=E,
∴B1C⊥平面BDE.
【方法点晴】本题主要考查线面平行的判定定理、线面垂直的判定定理,属于难题.证明线面平行的常用方法:①利用线面平行的判定定理,使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质,即两平面平行,在其中一平面内的直线平行于另一平面. 本题(1)是就是利用方法①证明的.

 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案【题目】“中国式过马路”存在很大的交通安全隐患.某调查机构为了解路人对“中国式过马路”的态度是否与性别有关,从马路旁随机抽取30名路人进行了问卷调查,得到了如下列联表:
男性 | 女性 | 合计 | |
反感 | 10 | ||
不反感 | 8 | ||
合计 | 30 |
已知在这30人中随机抽取1人抽到反感“中国式过马路”的路人的概率是 ![]() .
.
(Ⅰ)请将上面的列联表补充完整(在答题卡上直接填写结果,不需要写求解过程),并据此资料分析反感“中国式过马路”与性别是否有关?
(Ⅱ)若从这30人中的女性路人中随机抽取2人参加一活动,记反感“中国式过马路”的人数为X,求X的分布列和数学期望.
提示:可参考试卷第一页的公式.