题目内容
设三组实验数据(x1,y1),(x2,y2),(x3,y3)的回归直线方程是: |
| y |
 |
| b |
 |
| a |
 |
| b |
 |
| a |
 |
| b |
 |
| a |
 |
| b |
 |
| a |
 |
| b |
x1y1+x2y2+x3y3-3
| ||||
x12+x22-3
|
 |
| a |
. |
| y |
 |
| b |
(
. |
| x |
. |
| y |
| x | 2 | 3 | 4 | 5 | 6 | 7 |
| y | 4 | 6 | 5 | 6.2 | 8 | 7.1 |
(2)若|yi-(
 |
| b |
 |
| a |
分析:(1)根据表中的样本数据,可以求得
和
,利用求b的公式即可求得b的值,再根据回归方程必过点(
,
),即可求得a的值,从而求得答案;
(2)分别利用|yi-(
xi+
)|对后三组数据进行求解,判断对不等式是否成立,即可得到拟合“好点”的组数,从而确定后三组数据中拟合“好点”的概率.
. |
| x |
. |
| y |
. |
| x |
. |
| y |
(2)分别利用|yi-(
 |
| b |
 |
| a |
解答:解:(1)前三组数的平均数为
=3,
=5,
∵
=
,
∴
=
=
,
又∵回归方程
=
x+
必定过样本中心即(3,5),
∴5=
×3+
,解得
=
,
∴回归直线方程是
=
x+
;
(2)后三组数据分别代入|yi-(
xi+
)|中求解可得,
|6.2-3.5-0.5×5|=0.2≤0.2,
|8-3.5-0.5×6|=1.5>0.2,
|7.1-3.5-0.5×7|=0.1<0.2,
∵若|yi-(
xi+
)|≤0.2,即称(xi,yi)为(1)中回归直线的拟和“好点”,
∴拟和“好点”有2组,
∴后三组中拟合“好点”的概率P=
.
. |
| x |
. |
| y |
∵
 |
| b |
x1y1+x2y2+x3y3-3
| ||||
x12+x22-3
|
∴
 |
| b |
| 2×4+3×6+4×5-3×3×5 |
| 22+32+42-3×32 |
| 1 |
| 2 |
又∵回归方程
 |
| y |
 |
| b |
 |
| a |
∴5=
| 1 |
| 2 |
 |
| a |
 |
| a |
| 7 |
| 2 |
∴回归直线方程是
 |
| y |
| 1 |
| 2 |
| 7 |
| 2 |
(2)后三组数据分别代入|yi-(
 |
| b |
 |
| a |
|6.2-3.5-0.5×5|=0.2≤0.2,
|8-3.5-0.5×6|=1.5>0.2,
|7.1-3.5-0.5×7|=0.1<0.2,
∵若|yi-(
 |
| b |
 |
| a |
∴拟和“好点”有2组,
∴后三组中拟合“好点”的概率P=
| 2 |
| 3 |
点评:本题考查了回归方程的求解,求解时要注意回归方程必定过样本数据的中心(
,
).本题还考查了新定义问题,即给出一个新概念,利用题中所给的概念进行解题,关键是正确理解新定义的含义.考查了古典概型的求解,较有新意的一题.属于基础题.
. |
| x |
. |
| y |

练习册系列答案
相关题目
设三组实验数据(x1,y1).(x2,y2).(x3,y3)的回归直线方程是:y=bx+a,使代数式[y1-(bx1+a)]2+[y2-(bx2+a)]2+[y3-(bx3+a)]2的值最小时,a=
-b
,b=
,(
、
分别是这三组数据的横、纵坐标的平均数)
若有七组数据列表如图:
(Ⅰ)求上表中前三组数据的回归直线方程;
(Ⅱ)若|yi-(bxi+a)|≤0.2,即称(xi,yi)为(Ⅰ)中回归直线的拟和“好点”,求后四组数据中拟和“好点”的概率.
. |
| y |
. |
| x |
x1y1+x2y2+x3y3-3
| ||||
x12+x22+x32-3
|
. |
| x |
. |
| y |
若有七组数据列表如图:
| x | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| y | 4 | 6 | 5 | 6.2 | 8 | 7.1 | 8.6 |
(Ⅱ)若|yi-(bxi+a)|≤0.2,即称(xi,yi)为(Ⅰ)中回归直线的拟和“好点”,求后四组数据中拟和“好点”的概率.
设三组实验数据(x1,y1).(x2,y2).(x3,y3)的回归直线方程是:y=bx+a,使代数式[y1-(bx1+a)]2+[y2-(bx2+a)]2+[y3-(bx3+a)]2的值最小时, ,
,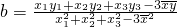 ,(
,( 、
、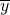 分别是这三组数据的横、纵坐标的平均数)
分别是这三组数据的横、纵坐标的平均数)
若有七组数据列表如图:
| x | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| y | 4 | 6 | 5 | 6.2 | 8 | 7.1 | 8.6 |
(Ⅱ)若|yi-(bxi+a)|≤0.2,即称(xi,yi)为(Ⅰ)中回归直线的拟和“好点”,求后四组数据中拟和“好点”的概率.
设三组实验数据(x1,y1).(x2,y2).(x3,y3)的回归直线方程是:y=bx+a,使代数式[y1-(bx1+a)]2+[y2-(bx2+a)]2+[y3-(bx3+a)]2的值最小时,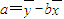 ,
,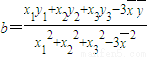 ,(
,(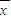 、
、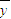 分别是这三组数据的横、纵坐标的平均数)
分别是这三组数据的横、纵坐标的平均数)
若有七组数据列表如图:
(Ⅰ)求上表中前三组数据的回归直线方程;
(Ⅱ)若|yi-(bxi+a)|≤0.2,即称(xi,yi)为(Ⅰ)中回归直线的拟和“好点”,求后四组数据中拟和“好点”的概率.
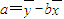 ,
,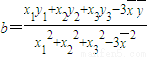 ,(
,(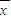 、
、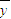 分别是这三组数据的横、纵坐标的平均数)
分别是这三组数据的横、纵坐标的平均数)若有七组数据列表如图:
| x | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| y | 4 | 6 | 5 | 6.2 | 8 | 7.1 | 8.6 |
(Ⅱ)若|yi-(bxi+a)|≤0.2,即称(xi,yi)为(Ⅰ)中回归直线的拟和“好点”,求后四组数据中拟和“好点”的概率.