题目内容
设三组实验数据(x1,y1).(x2,y2).(x3,y3)的回归直线方程是:y=bx+a,使代数式[y1-(bx1+a)]2+[y2-(bx2+a)]2+[y3-(bx3+a)]2的值最小时,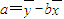 ,
,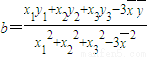 ,(
,(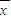 、
、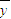 分别是这三组数据的横、纵坐标的平均数)
分别是这三组数据的横、纵坐标的平均数)若有七组数据列表如图:
| x | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| y | 4 | 6 | 5 | 6.2 | 8 | 7.1 | 8.6 |
(Ⅱ)若|yi-(bxi+a)|≤0.2,即称(xi,yi)为(Ⅰ)中回归直线的拟和“好点”,求后四组数据中拟和“好点”的概率.
【答案】分析:(I)根据所给的数据做出x与y的平均数,代入求线性回归方程系数的公式,利用最小二乘法做出结果,把样本中心点代入求出a的值,写出线性回归方程.
(II)本题是一个古典概型,试验发生包含的事件是4,检验出符合好点的数据,根据所给的表示式检验出符合条件的事件数,根据古典概型概率公式得到结果.
解答:解:(I)前三组数的平均数: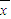 =3,
=3,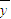 =5
=5
根据公式:b=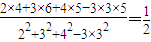
∴a=5- ×3=
×3=
∴回归直线方程是:y=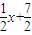
(II)由题意知本题是一个古典概型,
试验发生包含的事件是4,检验出符合好点的数据,
|6.2-3.5-0.5×5|=0.2≤0.2
|8-3.5-0.5×6|=1.5>0.2
|7.1-3.5-0.5×7|=0.1<0.2
|8.6-3.5-0.5×8|=1.1>0.2
综上,拟和的“好点”有2组,
∴“好点”的概率P=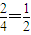
点评:本题考查线性回归方程的求法,考查最小二乘法求解线性回归方程的系数,考查古典概型及其概率公式.考查利用挨个检验的方法验证是否符合题意,本题是一个综合题目.
(II)本题是一个古典概型,试验发生包含的事件是4,检验出符合好点的数据,根据所给的表示式检验出符合条件的事件数,根据古典概型概率公式得到结果.
解答:解:(I)前三组数的平均数:
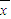 =3,
=3,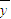 =5
=5根据公式:b=
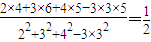
∴a=5-
 ×3=
×3=
∴回归直线方程是:y=
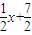
(II)由题意知本题是一个古典概型,
试验发生包含的事件是4,检验出符合好点的数据,
|6.2-3.5-0.5×5|=0.2≤0.2
|8-3.5-0.5×6|=1.5>0.2
|7.1-3.5-0.5×7|=0.1<0.2
|8.6-3.5-0.5×8|=1.1>0.2
综上,拟和的“好点”有2组,
∴“好点”的概率P=
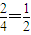
点评:本题考查线性回归方程的求法,考查最小二乘法求解线性回归方程的系数,考查古典概型及其概率公式.考查利用挨个检验的方法验证是否符合题意,本题是一个综合题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设三组实验数据(x1,y1).(x2,y2).(x3,y3)的回归直线方程是:y=bx+a,使代数式[y1-(bx1+a)]2+[y2-(bx2+a)]2+[y3-(bx3+a)]2的值最小时,a=
-b
,b=
,(
、
分别是这三组数据的横、纵坐标的平均数)
若有七组数据列表如图:
(Ⅰ)求上表中前三组数据的回归直线方程;
(Ⅱ)若|yi-(bxi+a)|≤0.2,即称(xi,yi)为(Ⅰ)中回归直线的拟和“好点”,求后四组数据中拟和“好点”的概率.
. |
| y |
. |
| x |
x1y1+x2y2+x3y3-3
| ||||
x12+x22+x32-3
|
. |
| x |
. |
| y |
若有七组数据列表如图:
| x | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| y | 4 | 6 | 5 | 6.2 | 8 | 7.1 | 8.6 |
(Ⅱ)若|yi-(bxi+a)|≤0.2,即称(xi,yi)为(Ⅰ)中回归直线的拟和“好点”,求后四组数据中拟和“好点”的概率.
设三组实验数据(x1,y1),(x2,y2),(x3,y3)的回归直线方程是:
=
x+
,使代数式[y1-(
x1+
)]2+[y2-(
x2+
)]2+[y3-(
x3+
)]2的值最小时,
=
,
=
-
x,
(
,
分别是这三组数据的横、纵坐标的平均数).若有六组数据列表如下:
(1)求上表中前三组数据的回归直线方程;
(2)若|yi-(
xi+
)|≤0.2,即称(xi,yi)为(1)中回归直线的拟和“好点”,求后三组数据中拟和“好点”的概率.
 |
| y |
 |
| b |
 |
| a |
 |
| b |
 |
| a |
 |
| b |
 |
| a |
 |
| b |
 |
| a |
 |
| b |
x1y1+x2y2+x3y3-3
| ||||
x12+x22-3
|
 |
| a |
. |
| y |
 |
| b |
(
. |
| x |
. |
| y |
| x | 2 | 3 | 4 | 5 | 6 | 7 |
| y | 4 | 6 | 5 | 6.2 | 8 | 7.1 |
(2)若|yi-(
 |
| b |
 |
| a |
设三组实验数据(x1,y1).(x2,y2).(x3,y3)的回归直线方程是:y=bx+a,使代数式[y1-(bx1+a)]2+[y2-(bx2+a)]2+[y3-(bx3+a)]2的值最小时, ,
,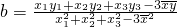 ,(
,( 、
、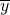 分别是这三组数据的横、纵坐标的平均数)
分别是这三组数据的横、纵坐标的平均数)
若有七组数据列表如图:
| x | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| y | 4 | 6 | 5 | 6.2 | 8 | 7.1 | 8.6 |
(Ⅱ)若|yi-(bxi+a)|≤0.2,即称(xi,yi)为(Ⅰ)中回归直线的拟和“好点”,求后四组数据中拟和“好点”的概率.