题目内容
设复数β=x+yi(x,y∈R)与复平面上点P(x,y)对应,且复数β满足条件|β+3|+(-1)n|β-3|=3a+(-1)na(其中n∈N*.常数a∈(
,3)),当n为奇数时,动点P(x,y)的轨迹为C1,当n为偶数时,动点P(x,y)的轨迹为C2,且两条曲线都经过点D(2,
),求轨迹C1与C2的方程?
| 3 |
| 2 |
| 2 |
分析:当n为奇数时,原等式可变形为,|β+3|-|β-3|=2a,当n为偶数时,原等式可变形为|β+3|+|β-3|=4a,代入点的坐标后联立两轨迹方程求解a的值,则答案可求.
解答:解:方法1:①当n为奇数时,|β+3|-|β-3|=2a,常数a∈ (
, 3),
轨迹C1为双曲线,其方程为
-
=1;
②当n为偶数时,|β+3|+|β-3|=4a,常数a∈ (
, 3),
轨迹C2为椭圆,其方程为
+
=1;
依题意得方程组
⇒
解得a2=3,
因为
<a<3,所以a=
,
此时轨迹为C1与C2的方程分别是:
-
=1,
+
=1.
方法2:依题意得
⇒
轨迹为C1与C2都经过点D(2,
),且点D(2,
)对应的复数β=2+
i,
代入上式得a=
,
即|β+3|-|β-3|=2
对应的轨迹C1是双曲线,方程为
-
=1;
|β+3|+|β-3|=4
对应的轨迹C2是椭圆,方程为
+
=1.
| 3 |
| 2 |
轨迹C1为双曲线,其方程为
| x2 |
| a2 |
| y2 |
| 9-a2 |
②当n为偶数时,|β+3|+|β-3|=4a,常数a∈ (
| 3 |
| 2 |
轨迹C2为椭圆,其方程为
| x2 |
| 4a2 |
| y2 |
| 4a2-9 |
依题意得方程组
|
|
因为
| 3 |
| 2 |
| 3 |
此时轨迹为C1与C2的方程分别是:
| x2 |
| 3 |
| y2 |
| 6 |
| x2 |
| 12 |
| y2 |
| 3 |
方法2:依题意得
|
|
轨迹为C1与C2都经过点D(2,
| 2 |
| 2 |
| 2 |
代入上式得a=
| 3 |
即|β+3|-|β-3|=2
| 3 |
| x2 |
| 3 |
| y2 |
| 6 |
|β+3|+|β-3|=4
| 3 |
| x2 |
| 12 |
| y2 |
| 3 |
点评:本题考查了轨迹方程,考查了分类讨论的数学思想方法,考查了方程组的解法,是中档题.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
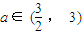 ),当n为奇数时,动点P(x、y)的轨迹为C1.当n为偶数时,动点P(x、y)的轨迹为C2.且两条曲线都经过点
),当n为奇数时,动点P(x、y)的轨迹为C1.当n为偶数时,动点P(x、y)的轨迹为C2.且两条曲线都经过点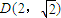 ,求轨迹C1与C2的方程;
,求轨迹C1与C2的方程;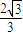 ,求实数x的取值范围.
,求实数x的取值范围.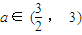 ),当n为奇数时,动点P(x、y)的轨迹为C1.当n为偶数时,动点P(x、y)的轨迹为C2.且两条曲线都经过点
),当n为奇数时,动点P(x、y)的轨迹为C1.当n为偶数时,动点P(x、y)的轨迹为C2.且两条曲线都经过点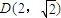 ,求轨迹C1与C2的方程;
,求轨迹C1与C2的方程;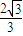 ,求实数x的取值范围.
,求实数x的取值范围.