题目内容
设复数β=x+yi(x,y∈R)与复平面上点P(x,y)对应.(1)若β是关于t的一元二次方程t2-2t+m=0(m∈R)的一个虚根,且|β|=2,求实数m的值;
(2)设复数β满足条件|β+3|+(-1)n|β-3|=3a+(-1)na(其中n∈N*、常数
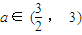 ),当n为奇数时,动点P(x、y)的轨迹为C1.当n为偶数时,动点P(x、y)的轨迹为C2.且两条曲线都经过点
),当n为奇数时,动点P(x、y)的轨迹为C1.当n为偶数时,动点P(x、y)的轨迹为C2.且两条曲线都经过点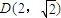 ,求轨迹C1与C2的方程;
,求轨迹C1与C2的方程;(3)在(2)的条件下,轨迹C2上存在点A,使点A与点B(x,0)(x>0)的最小距离不小于
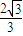 ,求实数x的取值范围.
,求实数x的取值范围.
【答案】分析:(1)由实系数方程虚根成对,利用韦达定理直接求出m的值.
(2)方法一:分n为奇数和偶数,化出a的范围,联立双曲线方程,求出a值,推出双曲线方程即可.
方法二:由题意分a的奇偶数,联立方程组,求出复数β,解出a,根据双曲线的定义求出双曲线方程.
(3)设点A的坐标,求出|AB|表达式,根据x范围,x的对称轴讨论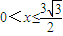 ,
,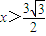 时,|AB|的最小值,不小于
时,|AB|的最小值,不小于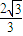 ,求出实数x的取值范围.
,求出实数x的取值范围.
解答:解:(1)β是方程的一个虚根,则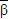 是方程的另一个虚根,(2分)
是方程的另一个虚根,(2分)
则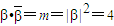 ,所以m=4(2分)
,所以m=4(2分)
(2)方法1:①当n为奇数时,|α+3|-|α-3|=2a,常数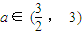 ),
),
轨迹C1为双曲线,其方程为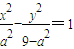 ;(2分)
;(2分)
②当n为偶数时,|α+3|+|α-3|=4a,常数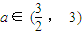 ),
),
轨迹C2为椭圆,其方程为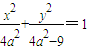 ;(2分)
;(2分)
依题意得方程组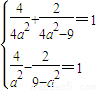
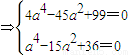
解得a2=3,
因为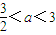 ,所以
,所以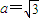 ,
,
此时轨迹为C1与C2的方程分别是: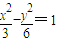 ,
,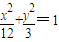 .(2分)
.(2分)
方法2:依题意得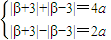
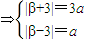 (2分)
(2分)
轨迹为C1与C2都经过点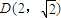 ,且点
,且点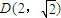 对应的复数
对应的复数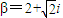 ,
,
代入上式得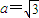 ,(2分)
,(2分)
即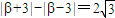 对应的轨迹C1是双曲线,方程为
对应的轨迹C1是双曲线,方程为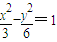 ;
;
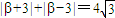 对应的轨迹C2是椭圆,方程为
对应的轨迹C2是椭圆,方程为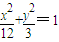 .(2分)
.(2分)
(3)由(2)知,轨迹C2: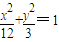 ,设点A的坐标为(x,y),
,设点A的坐标为(x,y),
则
=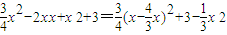 ,
,
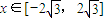 (2分)
(2分)
当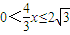 即
即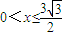 时,
时,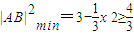
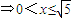
当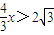 即
即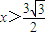 时,
时,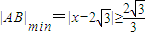
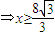 ,(2分)
,(2分)
综上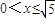 或
或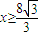 .(2分),
.(2分),
点评:本题考查复数的基本概念,轨迹方程,直线与圆锥曲线的综合问题,考查分类讨论思想,转化思想,是中档题.
(2)方法一:分n为奇数和偶数,化出a的范围,联立双曲线方程,求出a值,推出双曲线方程即可.
方法二:由题意分a的奇偶数,联立方程组,求出复数β,解出a,根据双曲线的定义求出双曲线方程.
(3)设点A的坐标,求出|AB|表达式,根据x范围,x的对称轴讨论
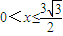 ,
,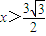 时,|AB|的最小值,不小于
时,|AB|的最小值,不小于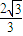 ,求出实数x的取值范围.
,求出实数x的取值范围.解答:解:(1)β是方程的一个虚根,则
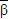 是方程的另一个虚根,(2分)
是方程的另一个虚根,(2分)则
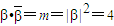 ,所以m=4(2分)
,所以m=4(2分)(2)方法1:①当n为奇数时,|α+3|-|α-3|=2a,常数
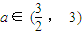 ),
),轨迹C1为双曲线,其方程为
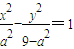 ;(2分)
;(2分)②当n为偶数时,|α+3|+|α-3|=4a,常数
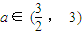 ),
),轨迹C2为椭圆,其方程为
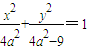 ;(2分)
;(2分)依题意得方程组
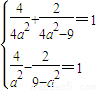
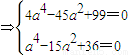
解得a2=3,
因为
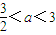 ,所以
,所以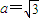 ,
,此时轨迹为C1与C2的方程分别是:
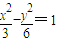 ,
,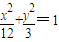 .(2分)
.(2分)方法2:依题意得
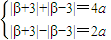
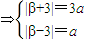 (2分)
(2分)轨迹为C1与C2都经过点
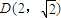 ,且点
,且点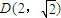 对应的复数
对应的复数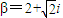 ,
,代入上式得
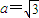 ,(2分)
,(2分)即
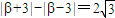 对应的轨迹C1是双曲线,方程为
对应的轨迹C1是双曲线,方程为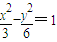 ;
;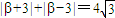 对应的轨迹C2是椭圆,方程为
对应的轨迹C2是椭圆,方程为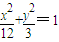 .(2分)
.(2分)(3)由(2)知,轨迹C2:
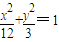 ,设点A的坐标为(x,y),
,设点A的坐标为(x,y),则

=
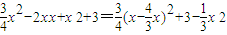 ,
,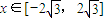 (2分)
(2分)当
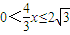 即
即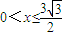 时,
时,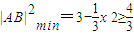
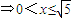
当
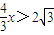 即
即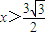 时,
时,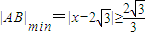
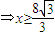 ,(2分)
,(2分)综上
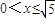 或
或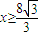 .(2分),
.(2分),点评:本题考查复数的基本概念,轨迹方程,直线与圆锥曲线的综合问题,考查分类讨论思想,转化思想,是中档题.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
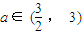 ),当n为奇数时,动点P(x、y)的轨迹为C1.当n为偶数时,动点P(x、y)的轨迹为C2.且两条曲线都经过点
),当n为奇数时,动点P(x、y)的轨迹为C1.当n为偶数时,动点P(x、y)的轨迹为C2.且两条曲线都经过点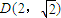 ,求轨迹C1与C2的方程;
,求轨迹C1与C2的方程;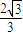 ,求实数x的取值范围.
,求实数x的取值范围.